Machine Learning (Coursera)

写在前面

本文是在自己的理解上总结了Coursera网站上吴恩达机器学习的课程内容，目录章节与课程有所出入。

线性回归

首先提出一个问题，如何用线性函数去预测房价。

解决这个问题的思路是可以采用简单的一维函数$ y=kx+b $去拟合训练数据，通过一个学习算法去学习最优的参数，使得通过这个函数所得到的结果与预想的结果相差无几，之后使用这个函数去预测新的值，即

$$h_\theta(x)=\theta_0+\theta_1x$$

那么如何去得到最优的参数呢？可以使用一个代价函数去评价当前参数是否是最优的，即

$$J(\theta_0,\theta_1)=\frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2$$

式中：$m$是训练数据的数量。

最终的目标就是使得这个代价函数越小，这时得到的参数就是最优的。

为了学习到更好的参数，从而使得代价函数最小，这里可以使用梯度下降法使得每次迭代后通过改变参数取值，使得代价函数下降，即

$$\theta_j=\theta_j-\alpha\cdot \frac{\partial}{\partial\theta_j}J(\theta_0,\theta_1)$$

梯度优化的过程：

1. 从设定的初始值开始
2. 不断的改变每个参数，使得代价函数的值有所降低
3. 直到得到最低的代价函数值，从而得到最优的参数

在迭代优化的过程中，需要计算完所有参数的优化值之后，再更新参数。否则如果每次计算完一个参数的梯度值就将更新参数的话，那么下一次计算代价函数的时候所得的值会跟之前不一样，导致不同步的参数更新。如下图

当梯度是正值时，说明函数曲线相对于最优点在上升，所以参数需要减去其值，向最优点靠近。

当梯度是负值时，说明函数曲线相对于最优点在下降，所以参数需要增加其值，向最优点靠近。

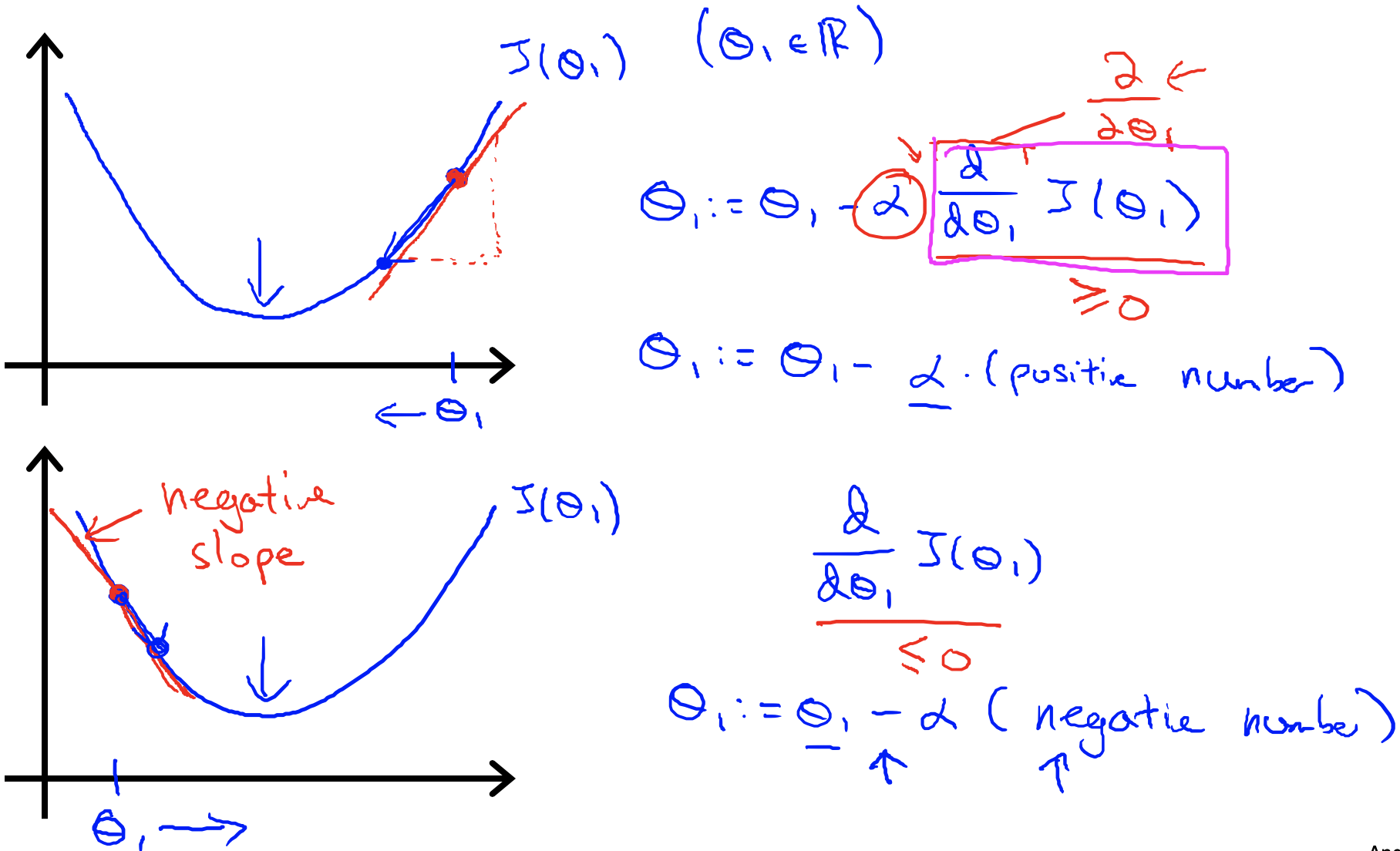
从图中可以看出，当学习率$ \alpha $特别小时，优化速度非常慢；当学习率$\alpha$特别大时，优化速度很快，但可能越过最优点，导致不收敛。

当每个特征值的范围相差过大时，可能会导致优化过程抖动不平缓，使得优化过程过慢。这时需要将每个特征归一化到同一尺度范围下，也就是特征缩放，将每个特征缩放到-1和1之间。即

$$x_i^{(j)}=\frac{x_i^{j}-\bar{x_i}}{S_i}$$

式中：$ S_i $可以为标准差，也可以为$\max(x_i)-\min(x_i)$。

如何选取学习率

在梯度优化的过程中，可以随着迭代次数的增加，适当降低学习率。因为当损失快要达到最优点时，需要减少步长来达到此最优点。

如果每次迭代之后，损失值的降低程度小于$10^{-3}$，那么可以认为当前函数已经收敛，可以停止训练。

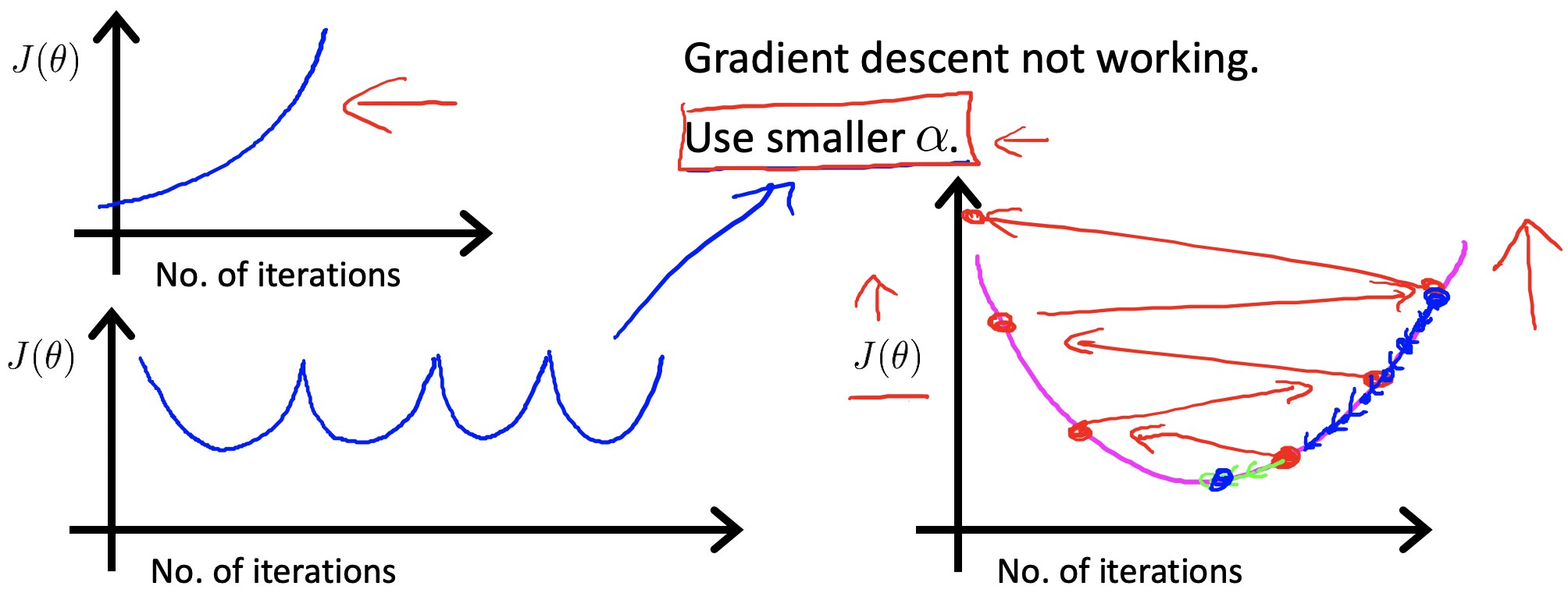
一个有效的学习率可以使得代价函数每次迭代后，损失都可以下降一些。

但如果学习率特别小的话，梯度下降的速度会变得非常慢。

当发生以上三种情况时，说明当前学习率过大，导致不收敛的情况，需要选择一个更小的学习率来完成迭代。 一个建议的学习率选择过程为： > …, 0.001, 0.003, 0.01, 0.03, 0.1, 0.3, 1, ... 前面提到的线性回归目标函数中，仅使用了一次项，当使用多项式回归去拟合函数时，即$h_\theta(x)=\theta_0+\theta_1x+\theta_2x^2+\theta_3x^3+\cdots$，当使用多项式回归方法时，数据的标准化工作就显得尤为重要。 这时，就可以使用常规等式法去求解最优的参数，使得损失函数为零。 $$ \frac{\partial}{\partial\theta_j}J(\theta)=0\ \ \ \ \ \ \ \ -> \theta=(x^Tx)^{-1}x^Ty $$ 以下是这两种方法的区别和优缺点： | Gradient descent | Normal equation | | -------------------------------- | ------------------------------------------ | | 需要选择学习率 | 不需要选择学习率 | | 迭代次数多 | 没有迭代的过程 | | 特征数量较多时也能达到很好的效果 | 由于存在逆运算，特征数量较多时计算速度太慢 | > 当特征矩阵不可逆时，说明有冗余的特征，需要对特征进行处理或使用正则化。 ### 逻辑回归 逻辑回归是回归问题的离散化，目的是解决分类问题。 分类任务需要确切的结果值，如0代表不是，1代表是。逻辑回归的结果$ 0\le h_\theta(x)\le1 $，这就需要一个边界去判别在什么范围内结果为0，什么范围内结果为1。这就引出了激活函数： $$ h_\theta(x)=\frac{1}{1+e^{-\theta^Tx}} $$ 这个激活函数是sigmoid函数，它能有效将函数值分在两个区间内。 之后就是确定一个决策边界： 当$h_\theta(x)\ge0.5,\theta^Tx\ge0$时，$y=1$ 当$h_\theta(x)\le0.5,\theta^Tx\le0$时，$y=0$ 如何去选择参数来将结果接近于真实值？这时需要一个目标函数： $$ J(\theta)=\frac{1}{2m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})^2 $$ 如果采用上述线性回归代价函数的话，由于非线性激活函数的引入，结果会产生"非凸形"，如下图

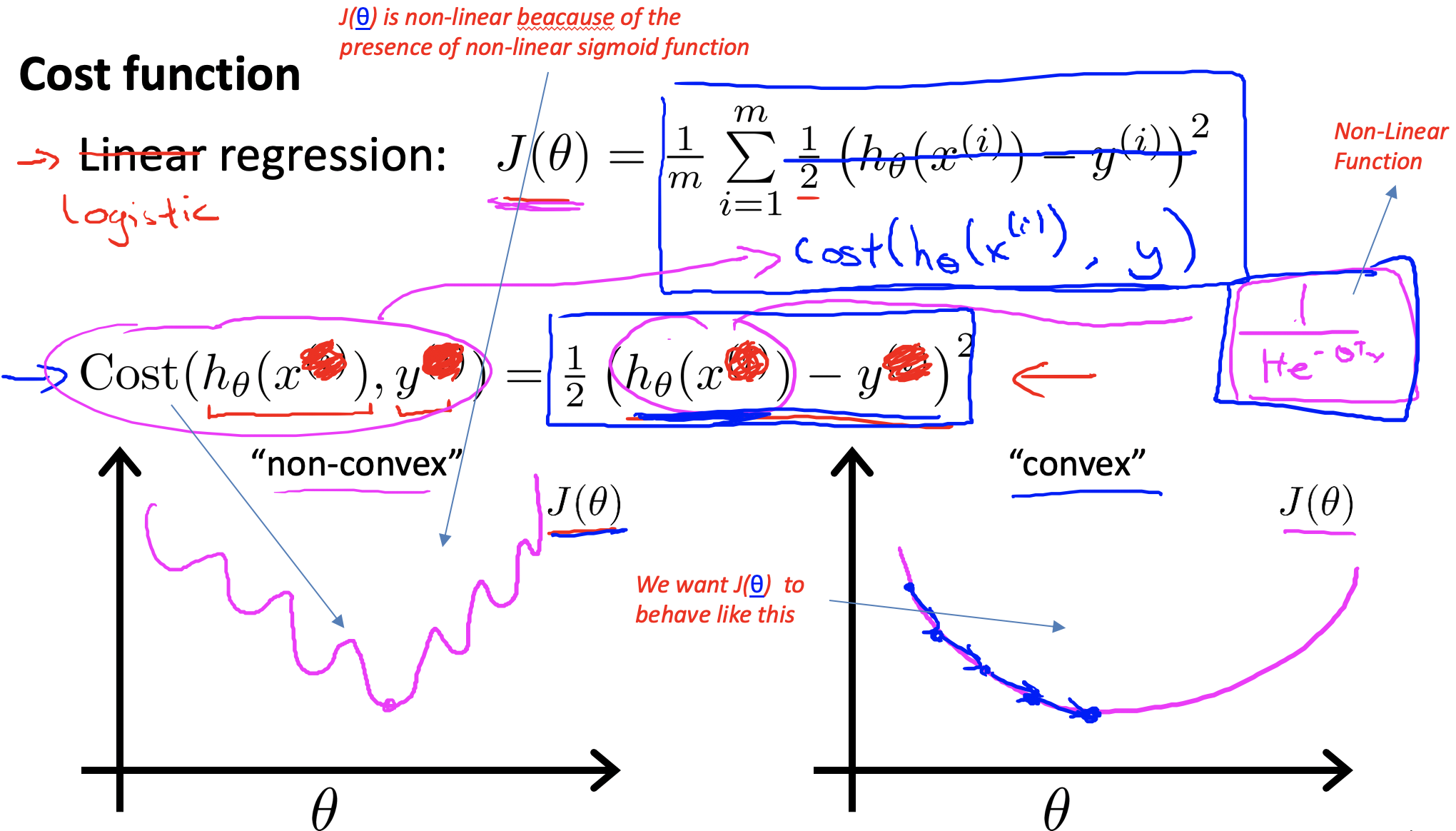
这时就需要另一种代价函数，因为结果值无非是0和1，所以针对这两种情况可以建立一个代价函数。

$$Cost(h_\theta(x),y)=\begin{cases}-\log{(h_\theta(x))}\ \ \ \ \ \ \ \ \ \ if\ y=1 \\ -\log{(1-h_\theta(x))}\ \ \ if\ y=0 \end{cases}$$

当预测结果和真实结果一致时，我们希望损失为零；当不一致时，我们希望损失变得很大。

因为$y$仅可能为1或者0，所以可以将上式变为：

$$J(\theta)=-y\log{(h_\theta(x))}-(1-y)\log{(1-h_\theta(x))}$$

使用梯度下降法去降低损失函数，从而优化参数。

$$\theta=\theta-\alpha\frac{\partial}{\partial\theta}J(\theta)$$

通过上述优化方法可能会产生两个不好的结果，一个是过拟合，造成低偏差、高方差的现象，一个是欠拟合，造成高偏差、低方差的现象。

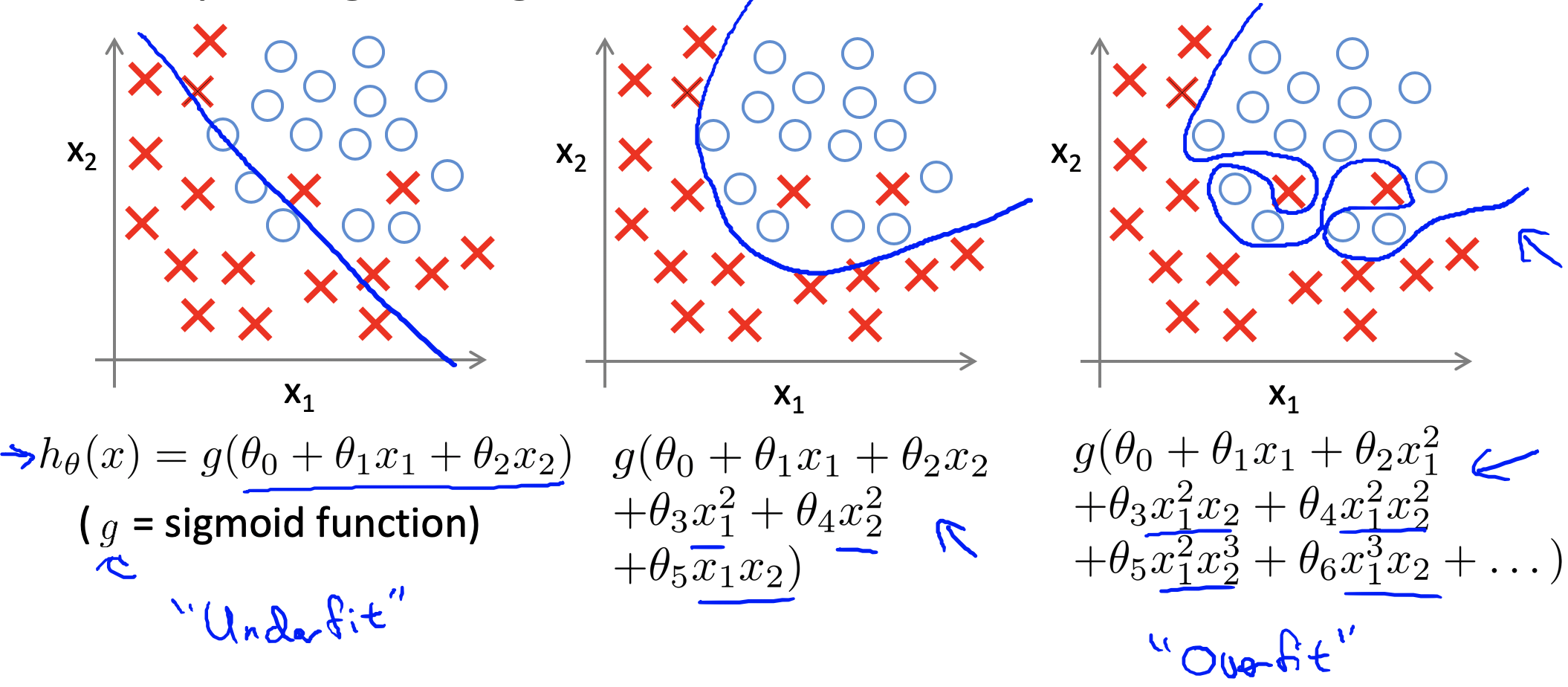
解决过拟合有以下几种方法：

1. 降低特征的数量（可以手动或者通过算法选择一些特征，抛弃一些特征）
2. 正则化（保留所有特征，但降低每个特征对结果的影响程度）

正则化就是在损失函数的最后加入一些惩罚项，比如加入$100\times\theta_3$，这时如果$\theta_3$变的大就会严重增大损失函数的值，通过优化手段就可以让函数自己去减少此参数的值，从而降低此参数的影响力，完成优化的效果。

$$J(\theta)=\frac{1}{2m}[\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})^2+\lambda\sum^n_{j=1}\theta^2_j]$$

这里正则项是不包含$\theta_0$参数的，可以把它理解成一个偏置。

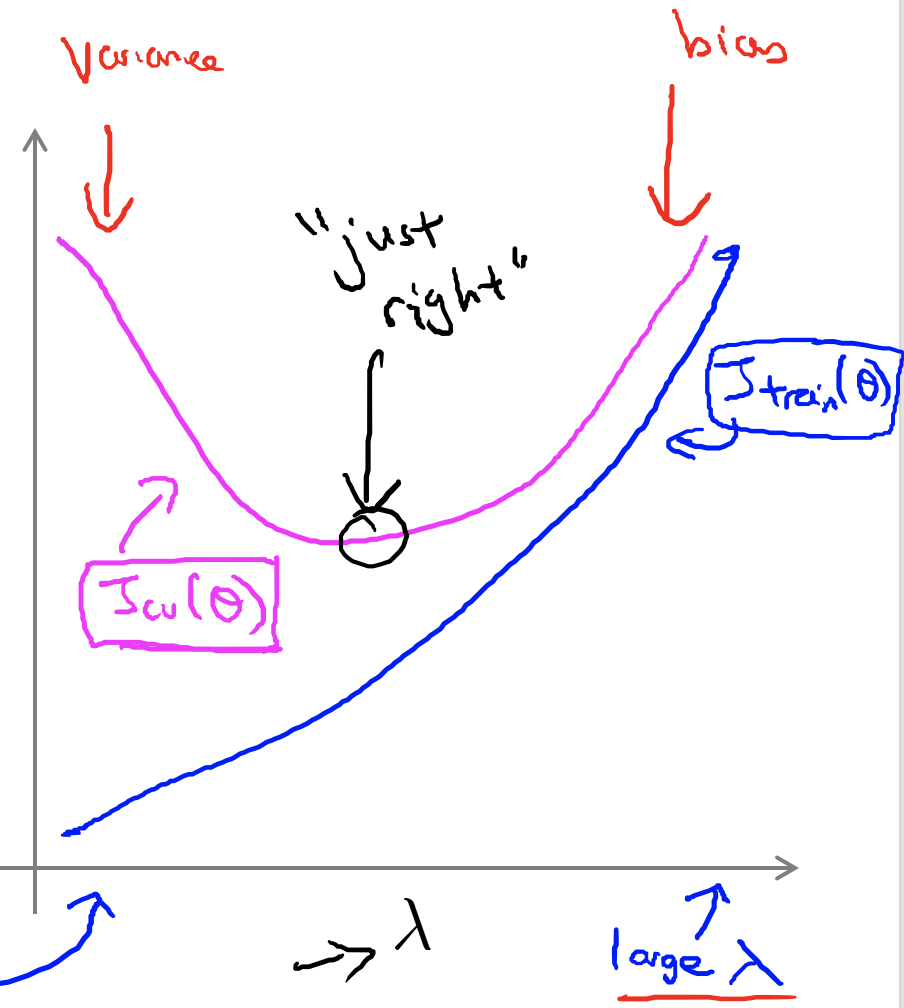
• 如果$\lambda$过大，会造成抑制参数的效果变得很强，产生欠拟合的效应。

• 如果$\lambda$过小，会造成抑制参数的效果变得很弱，产生过拟合的效应。

那么，之后的梯度下降过程就变成了：

$$\theta_0=\theta_0-\alpha\frac{1}{m}(\frac{\partial}{\partial\theta_0}J(\theta))=\theta_0-\alpha\frac{1}{m}(\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})x_0^{(i)})$$ $$\theta_j=\theta_j-\alpha[\frac{1}{m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}-\frac{\lambda}{m}\theta_j]=\theta_j(1-\alpha\frac{\lambda}{m})-\alpha\frac{1}{m}\sum^m_{i=1}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}$$

由于$ 1-\alpha\frac{\lambda}{m}<1 $，所以梯度下降的过程中参数会一直减小。

神经网络

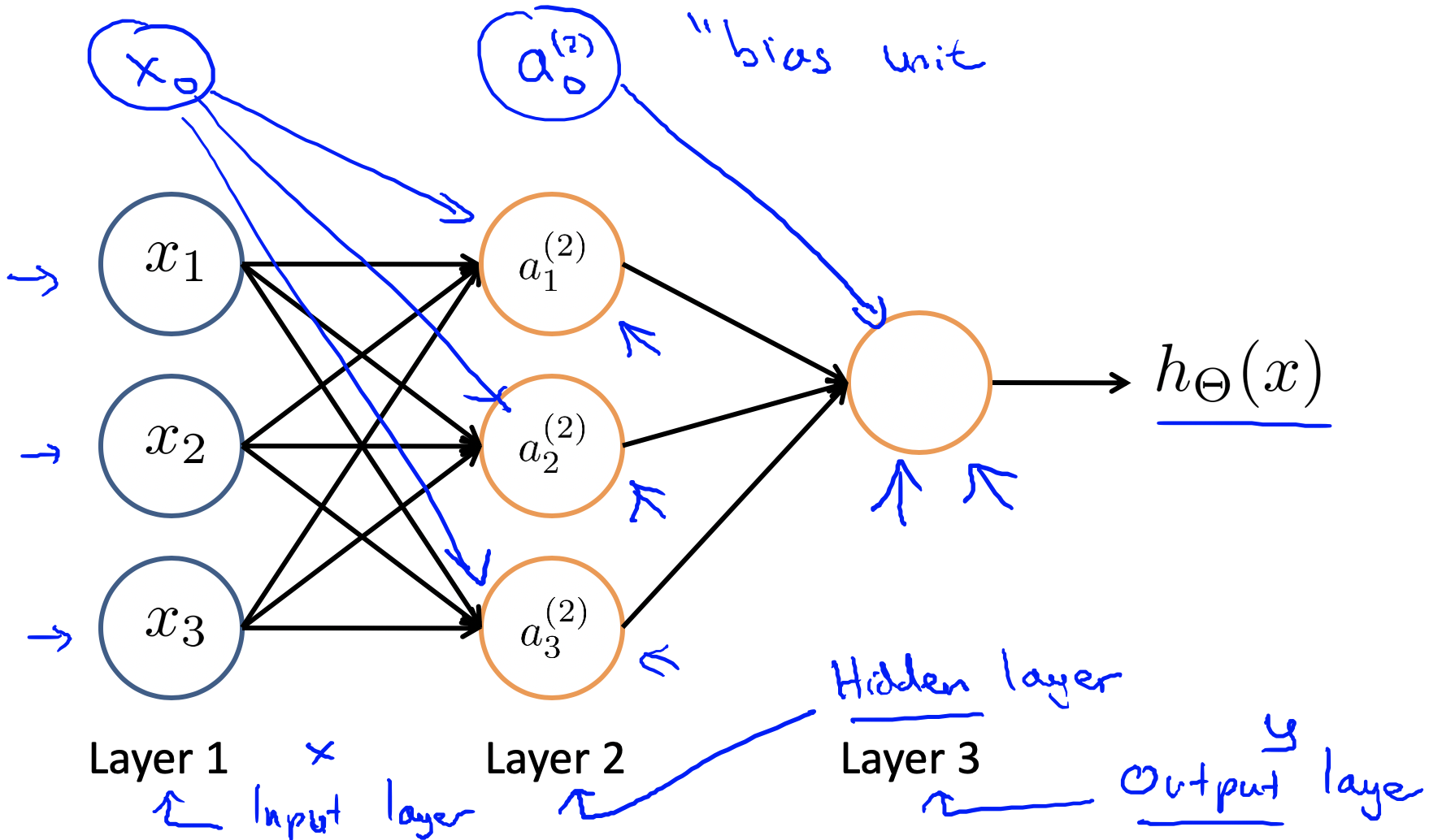
上图是一个简单神经网络的实例，图中有输入单元、隐藏单元和输出单元，而网络的输出即为：

$$h_\theta(x)=a_1^{(3)}=g(\theta_{10}^{(2)}\cdot a_0^{2}+\theta_{11}^{(2)}\cdot a_1^{(2)}+\theta_{12}^{(2)}\cdot a_2^{(2)}+\theta_{13}^{(2)}\cdot a_3^{(2)})$$

如果网络中的第$j$层有$s_j$个单元，第$j+1$层有$s_{j+1}$个单元，那么第$j$层的参数$\theta_j$就会有$s_{j+1}\times(s_j+1)$个单元。

神经网络可以完成一种非线性的计算——异或：

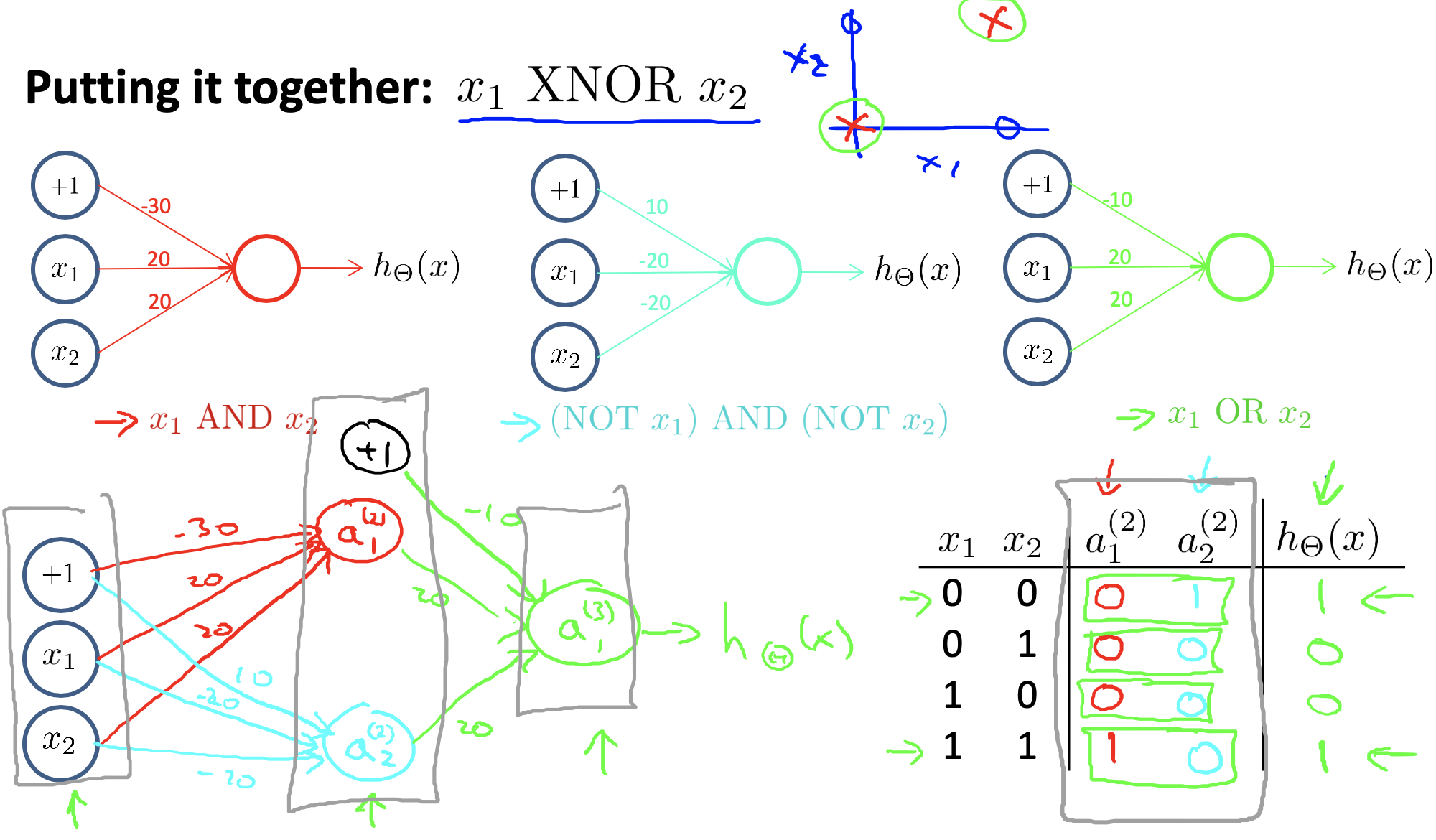
神经网络可以完成多类别的表达：

$$y^{(i)}:\begin{bmatrix}1 \\0 \\. \\. \\. \\0 \end{bmatrix}\begin{bmatrix}0 \\1 \\. \\. \\. \\0 \end{bmatrix} … \begin{bmatrix}0 \\0 \\. \\. \\. \\1 \end{bmatrix}$$

上式中第一个矢量代表第一类，第二个矢量代表第二类，以此类推，最后一个矢量代表最后一类，类别的个数和矢量中元素的个数一致。

神经网络的代价函数如下：

$$J(\theta)=-\frac{1}{m}[\sum^m_{i=1}\sum^K_{k=1}y_k^{(i)}\log{(h_\theta(x_k^{(i)}))}+(1-y_k^{(i)})\log{(1-h_\theta(x_k^{(i)}))}]+\frac{\lambda}{2m}\sum^{L-1}_{l=1}\sum^{s_l}_{i=1}\sum^{s_{l+1}}_{j=1}(\theta_{ji}^{(l)})^2$$

式中：$ (h_\theta(x))_i $表示第$i$层的输出，$m$表示特征的个数，$L$表示神经网络的层数，输出代表第1层，$s_l$表示第$l$层不包含偏置之后的单元数。

那么，接下来输出结果的大概计算过程如下：

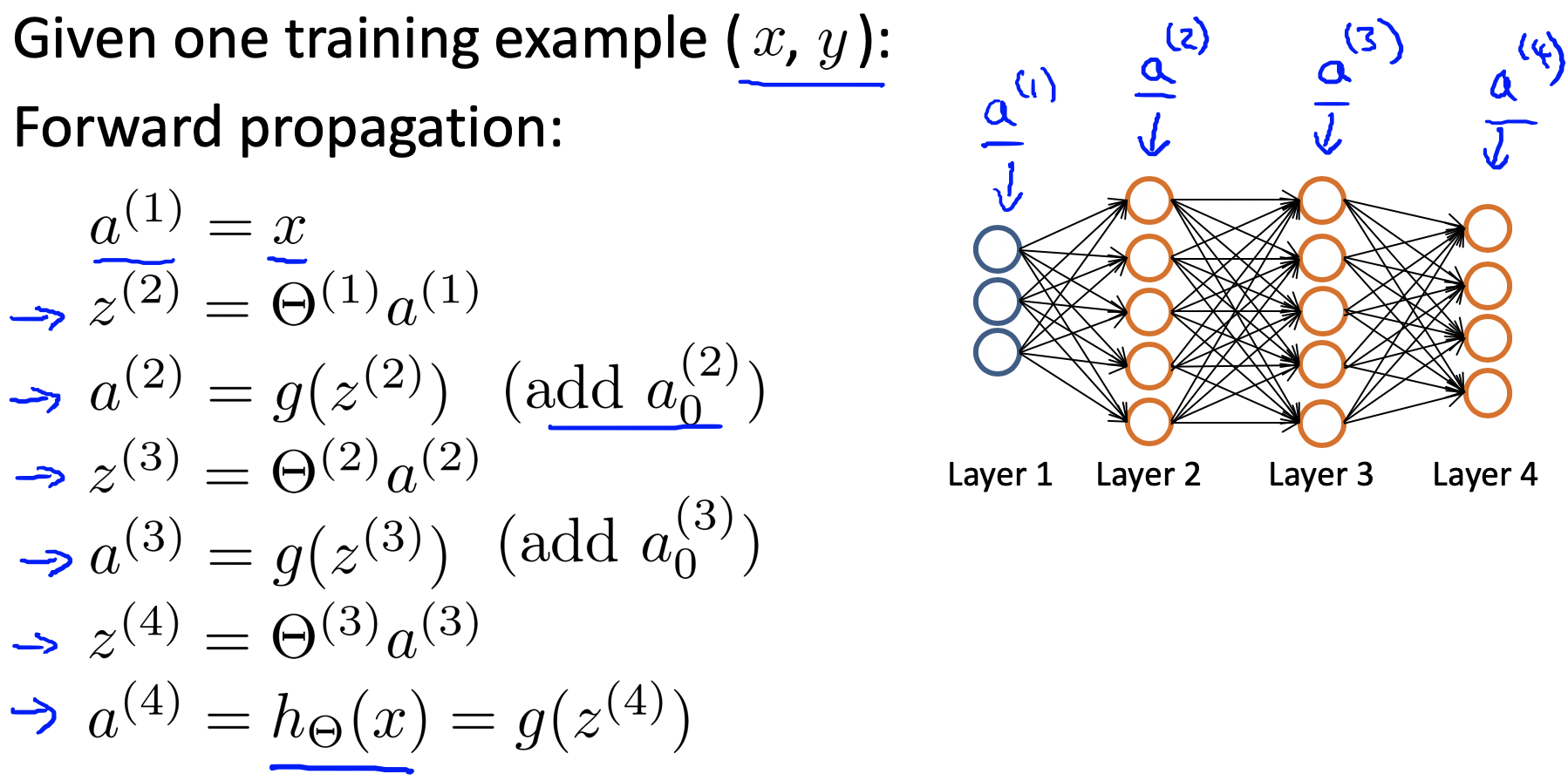
假设$\delta_j^{(l)}$表示第$l$层第$j$个单元的损失，那么首先最后一层中某个单元的损失为

$$\delta^{(4)}=a^{(4)}-y$$

因为输出结果与最后一层之间没有激活函数，那么接下来每一层的传播如下

$$\delta^{(3)}=(\theta^{(3)})^T\delta^{(4)}.*g'(z^{(3)})$$

具体过程如下

在梯度优化的过程中可能由于编程错误而导致一些不好的结果，可能导致最终函数无法收敛。如果在训练的过程中能够检查梯度下降是否正确，可以在训练的时候避免这些错误。

$$\frac{\partial}{\partial\theta_i}J(\theta)\approx\frac{J(\theta+\epsilon)-J(\theta-\epsilon)}{2\epsilon}$$

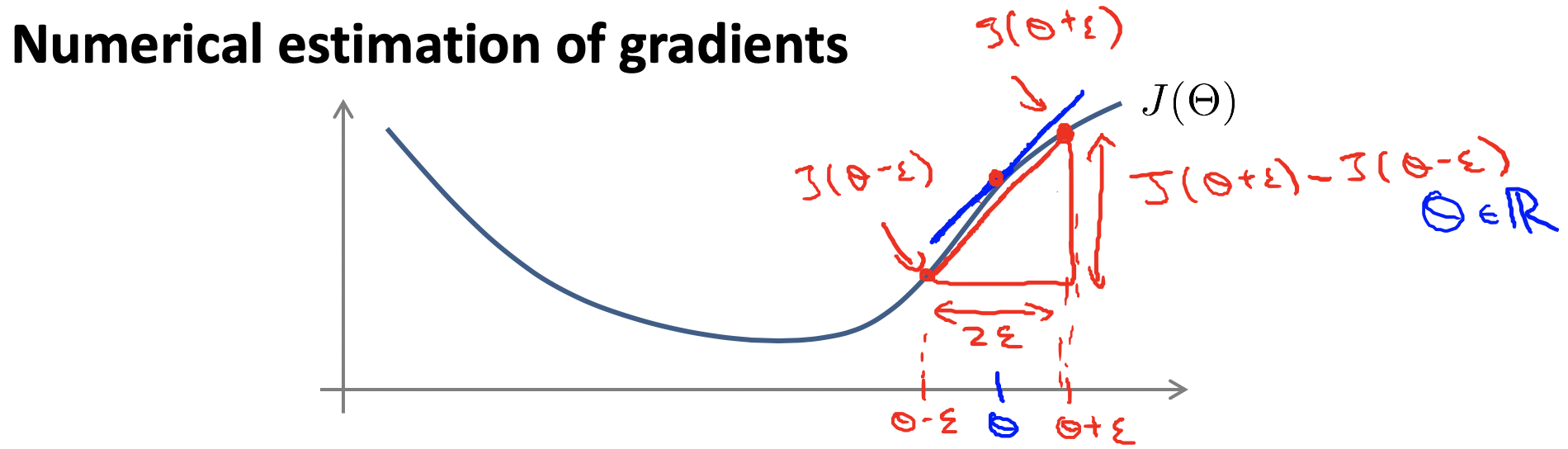
所以在求解多个参数最优解的过程中，可以分别对每个参数进行梯度检查工作，检查某个参数的梯度下降过程是否正确，确保反向传播的结果和梯度检查的结果一致。不过此项工作仅在训练过程中使用，测试过程需要去掉这一部分。

参数初始化

如果将参数初始化为零向量，则会导致$ a_1^{(2)}=a_2^{(2)} $，那么$ \delta_1^{(2)}=\delta_2^{(2)} $，所以会造成没有更新参数的结果，传回的梯度会零。

所以参数初始化有一个原则，就是切忌将参数初始化成对称的结构。

小结

训练神经网络的主要过程如下：

1. 随机初始化参数权重
2. 计算前向传播并得到结果
3. 将结果带入代价函数计算其损失值
4. 通过对损失值求导来反向传播参数的损失
5. 使用梯度检查方法检查反向传播的结果和梯度估计的结果是否一致
6. 利用梯度下降和优化方法对反向传播进行操作，从而通过调整参数来最小化代价函数

应用机器学习过程中的一些建议

当你应用正则化线性回归到实际任务中时，如果在预测时产生了很大的错误，可以尝试以下措施：

• 增加训练数据——处理高方差问题
• 降低特征冗余——处理高方差问题
• 增加额外的特征——处理高偏差问题
• 加入一下多项式特征——处理高偏差问题
• 增加正则化系数的值——处理高方差问题
• 减小正则化系数的值——处理高偏差问题

数据集设置建议

将数据集分为三个部分：训练集、评估集、测试集，并通过交叉验证去得到最好的参数。

上图是正则化参数与模型好坏的比较趋势，当参数特别小时，训练集错误率很低，但评估集错误率就很高。随着参数的增加，训练集错误率会提升，而评估集错误率会先下降再上升。因为当偏差高到一定程度时，模型效果就会非常差，几乎完成不了任何任务。所以一个恰到好处的正则化参数会平衡训练集误差和评估集误差，最终得到一个较好的模型。

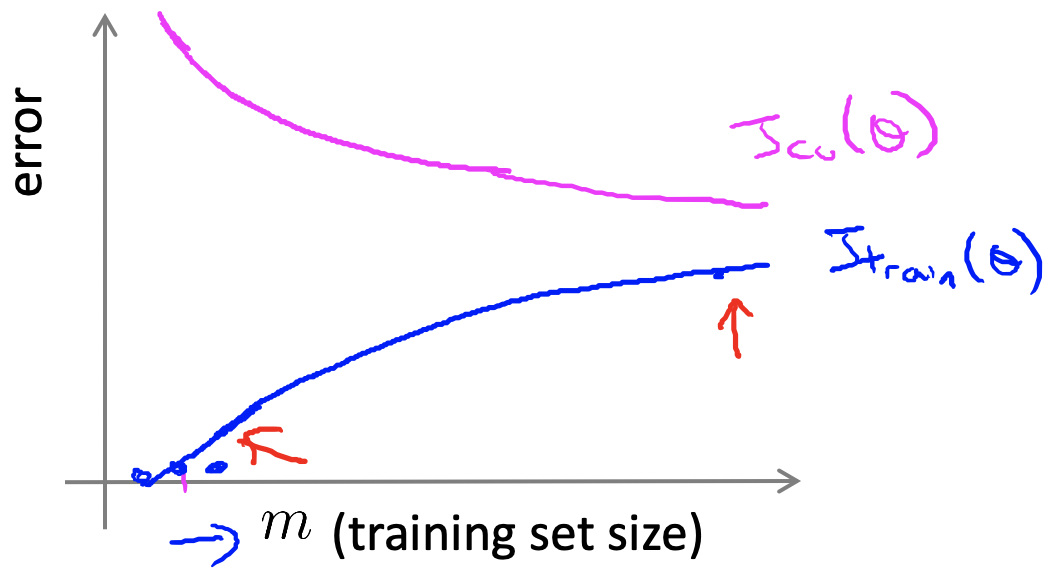
上图是训练集大小和模型好坏的比较趋势，随着训练集的增加，模型的偏差会慢慢增加，而方差会慢慢减小，最终两个误差会趋于平和，达到较好的效果。

神经网络复杂度问题

当训练一个小型神经网络的时候，参数会比较少，计算效率比较高，但可能会有欠拟合的问题。

当训练一个大型神经网络的时候，参数会比较多，计算效率比较低，而且会有过拟合的问题，可以采用正则化去降低过拟合的影响。

误差分析

评估一个模型的好坏时可以采用准确率和召回率指标。

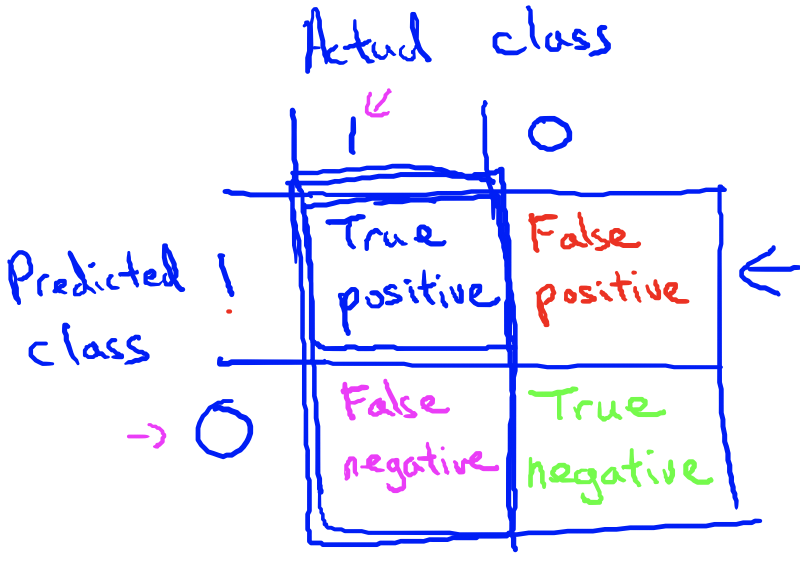
准确率表示所有模型预测结果为1时，预测正确的比例，即

$$Precision=\frac{True\ positive}{Predicted\ positive}=\frac{True\ positive}{True\ positive+False\ positive}$$

召回率表示所有实际结果为1时，预测正确的比例，即

$$Recall=\frac{True\ positive}{Actual\ positive}=\frac{True\ positive}{True\ positive+False\ negative}$$

如何去综合上述两个评估指标？

$$F_1\ Score=2\cdot\frac{P\cdot R}{P+R}$$

如何设计一个具有高准确率的学习系统？

It’s not who has the best algorithm that wins. It’s who has the most data.

支持向量机

通过对逻辑回归中代价函数的分析可知，当标签为正样本时，代价函数如上左图所示，当标签为负样本时，代价函数如上右图所示。 为了让损失值降到最低，当样本是正样本时，我们希望通过激活函数之后的$g(x)$即$sigmoid(\theta^Tx)\ge0$。从上图可以看出，为了满足条件，$z$的值可以大于0，只要近似大于1就可以满足，那么这里就存在一个边界区间的问题。

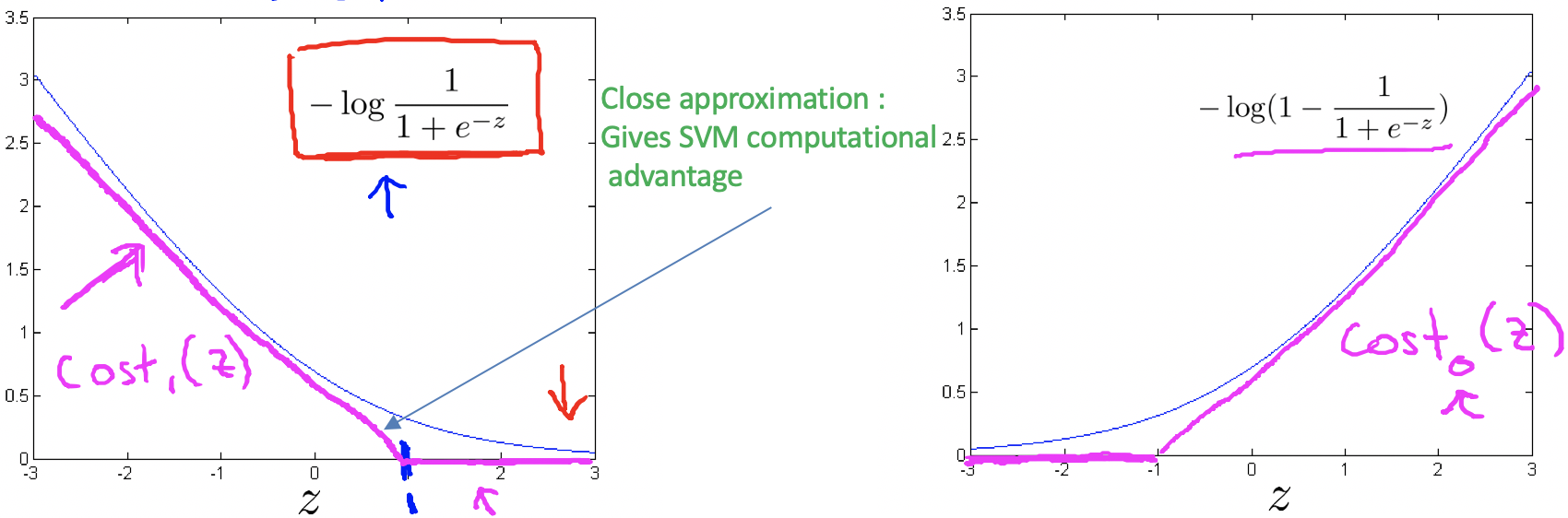
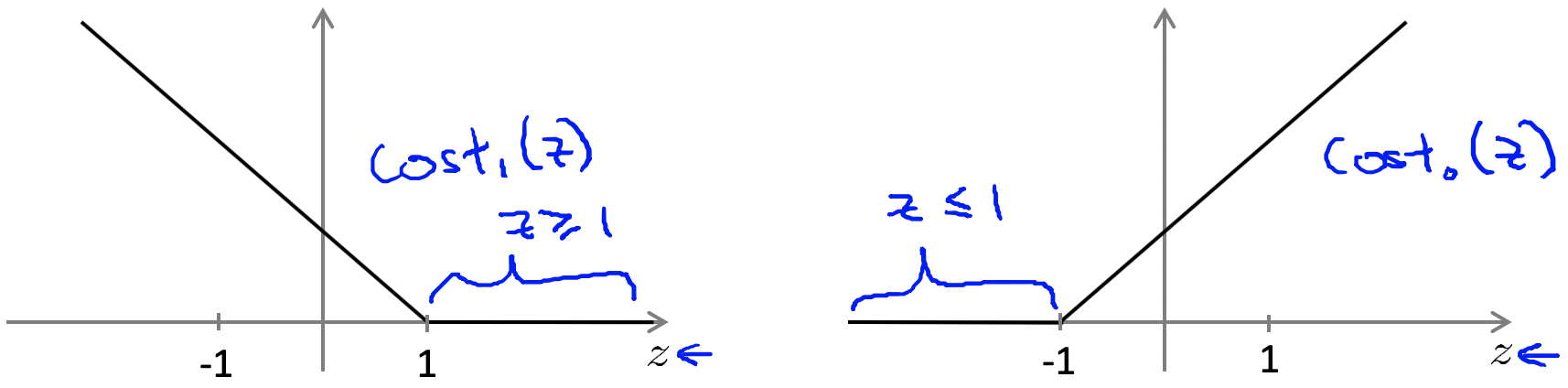
逻辑回归代价函数的形式为：$ A+\lambda B $，我们更加关注第二项$B$

SVM代价函数的形式为：$C\cdot A+B$，我们更加关注第一项$A$，即

$$\min\limits_\theta C\sum^m_{i=1}[y^{(i)}cost_1(\theta^Tx^{(i)})+(1-y^{(i)})cost_0(\theta^Tx^{(i)})]+\frac{1}{2}\sum^n_{i=1}\theta^2_j$$

支持向量机为了解决上述一个边界区间的问题，将代价函数进行了修改。从上图可以看出，当$z$小于等于1时，$cost$函数严格大于0。所以SVM与逻辑回归最大的区别就在于

$$\begin{cases}y=1\ \ \ \theta^Tx\ge1\ \ \ not\ \ge0\\ y=0\ \ \ \theta^Tx\le1\ \ \ not\ \le0\end{cases}$$

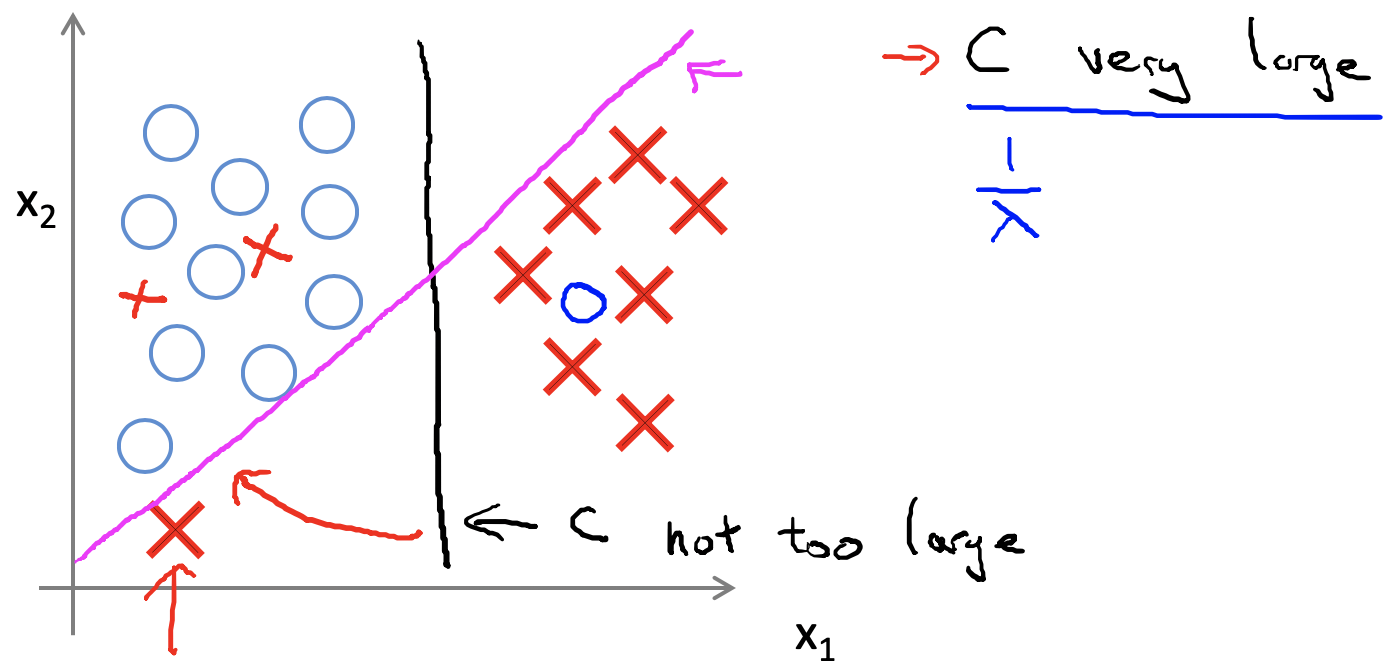
当$C$很大时，希望$A$这部分函数值趋于0，也就是可以让$cost$函数这部分趋于0，从而控制参数$\theta$的选取。下图可以看出$C$的选取对于边界的影响。

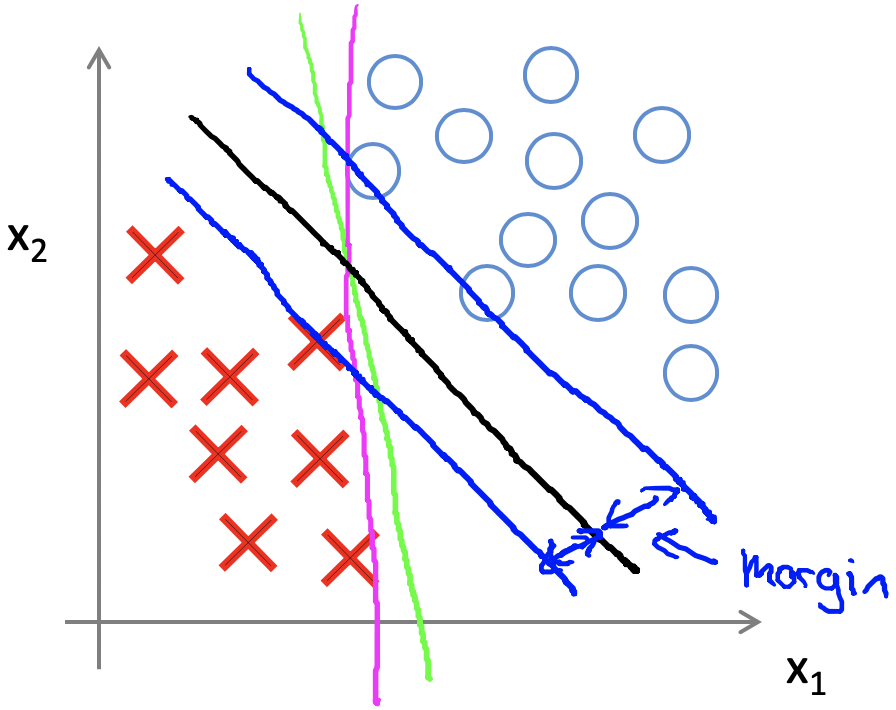
最大边界理论

SVM的决策边界为$\min\limits_\theta\frac{1}{2}\sum^n_{j=1}\theta^2_j=\frac{1}{2}||\theta||^2$，约束条件为$ \begin{cases}\theta^Tx\ge0\ \ \ \ if\ y=1\\ \theta^Tx\le-1\ if\ y=0\end{cases} $

$$\theta^Tx^{(i)}=p^{(i)}\cdot ||\theta||=\theta_1x_1^{(i)}+\theta_2x_2^{(i)}$$

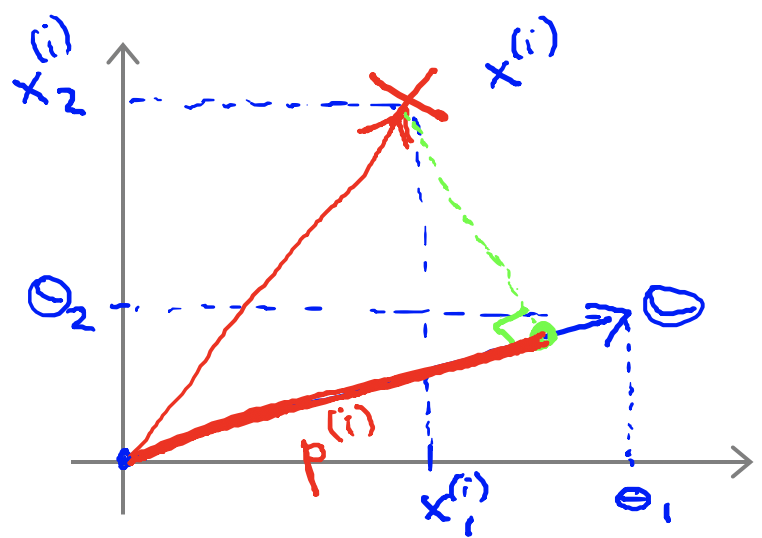
式中：$p^{(i)}$是$x$在$\theta$上的投影。

若想$||\theta||$的值越小，就应该使得$p^{(i)}$的值越大，当向量$\theta$的长度等于$p$时，也就得到了最大间隔，即最大边界。

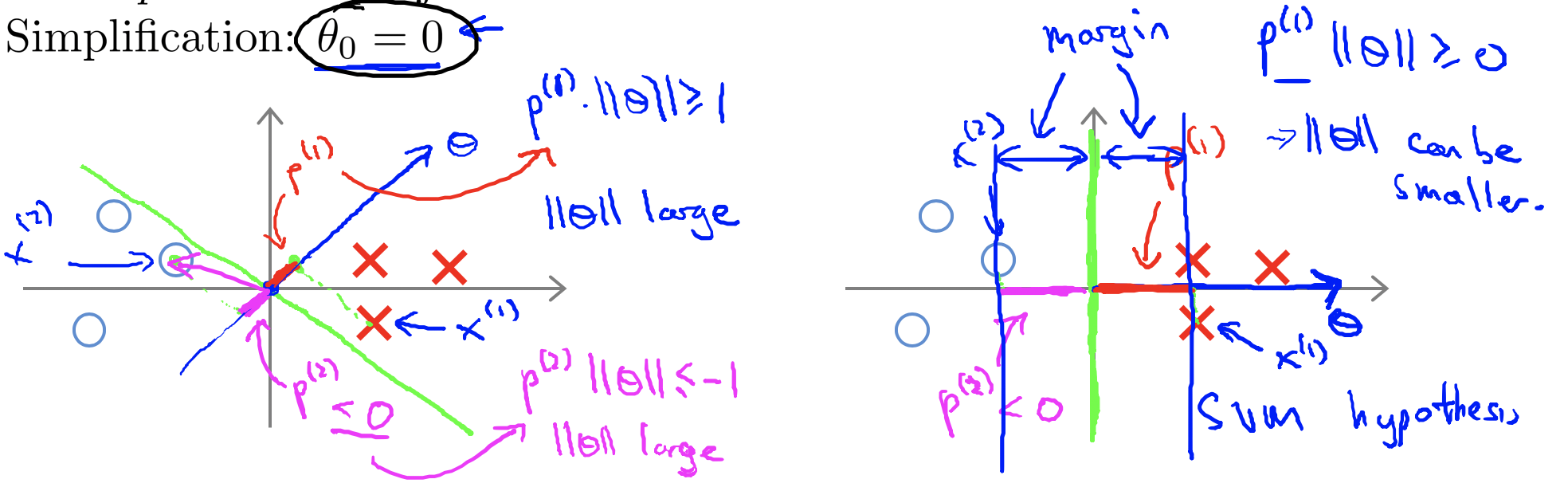
以上仅可以解决线性可分的情况，当遇到线性不可分的情况，就需要加入核函数。

核函数

举个例子讲解一下什么是核函数：

例如当进行kNN分类时，输入一个数据x，必须计算它与每个聚类中心数据点的相似度来决定它被分到哪一类别中，而这个计算相似度的函数就是核函数。

其中聚类中心也称landmarks。

当加入核函数$f(x)$之后，预测值为正样本的情况为$\theta^Tf\ge0(\theta_0f_0+\theta_1f_1+\theta_2f_2+…+\theta_mf_m)$，SVM的代价函数可以写为

$$\min\limits_\theta C\sum^m_{i=1}[y^{(i)}cost_1(\theta^Tf^{(i)})+(1-y^{(i)})cost_0(\theta^Tf^{(i)})]+\frac{1}{2}\sum^m_{i=1}\theta^2_j$$

式中：$C=\frac{1}{\lambda}$，越大导致高偏差，越小导致高方差。

SVM与逻辑回归的区别

• 当特征数远远大于训练样本数时，选择逻辑回归或者不加核函数的SVM方法
• 当特征数远远小于训练样本数时，需要增加一些特征，并选择逻辑回归或者不加核函数的SVM方法
• 当特征数非常少，训练样本数适当时，选择加核函数的SVM方法

非监督学习

非监督学习是一个聚类算法，事前并不需要知道数据的标签，只是根据数据的特征和分布进行类别聚类。

K-means

输入：聚类中心个数k和训练数据

步骤：

随机初始化聚类中心
Repeat{
	for i = 1 ~ m
		c(i) = 距离最近的聚类中心 min||x-u||
	for k = 1 ~ K
		更新聚类中心，取平均值
}

此算法需要优化的目标函数为

$$J(c^{(i)},…,c^{(m)},\mu_1,…,\mu_K)=\frac{1}{m}\sum^m_{i=1}||x^{(i)}-\mu_{c^{(i)}}||^2$$

式中：$c^{(i)}$为当前数据$x^{(i)}$当前所从属的聚类中心，$\mu_k$表示聚类中心，$\mu_{c^{(i)}}$表示当前数据$x^{(i)}$所属类别的聚类中心点。

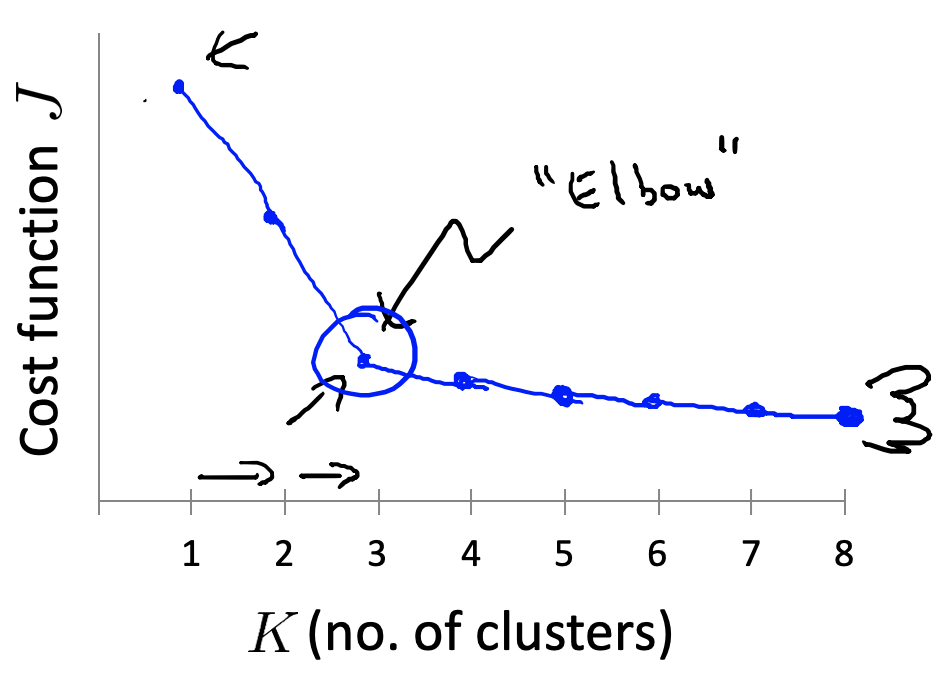
在选取k值方面，可以选取多个k值，并分别计算代价函数的结果值，如上图。图中有一个肘点，即k=3的情况，可以认为是最优的选择。

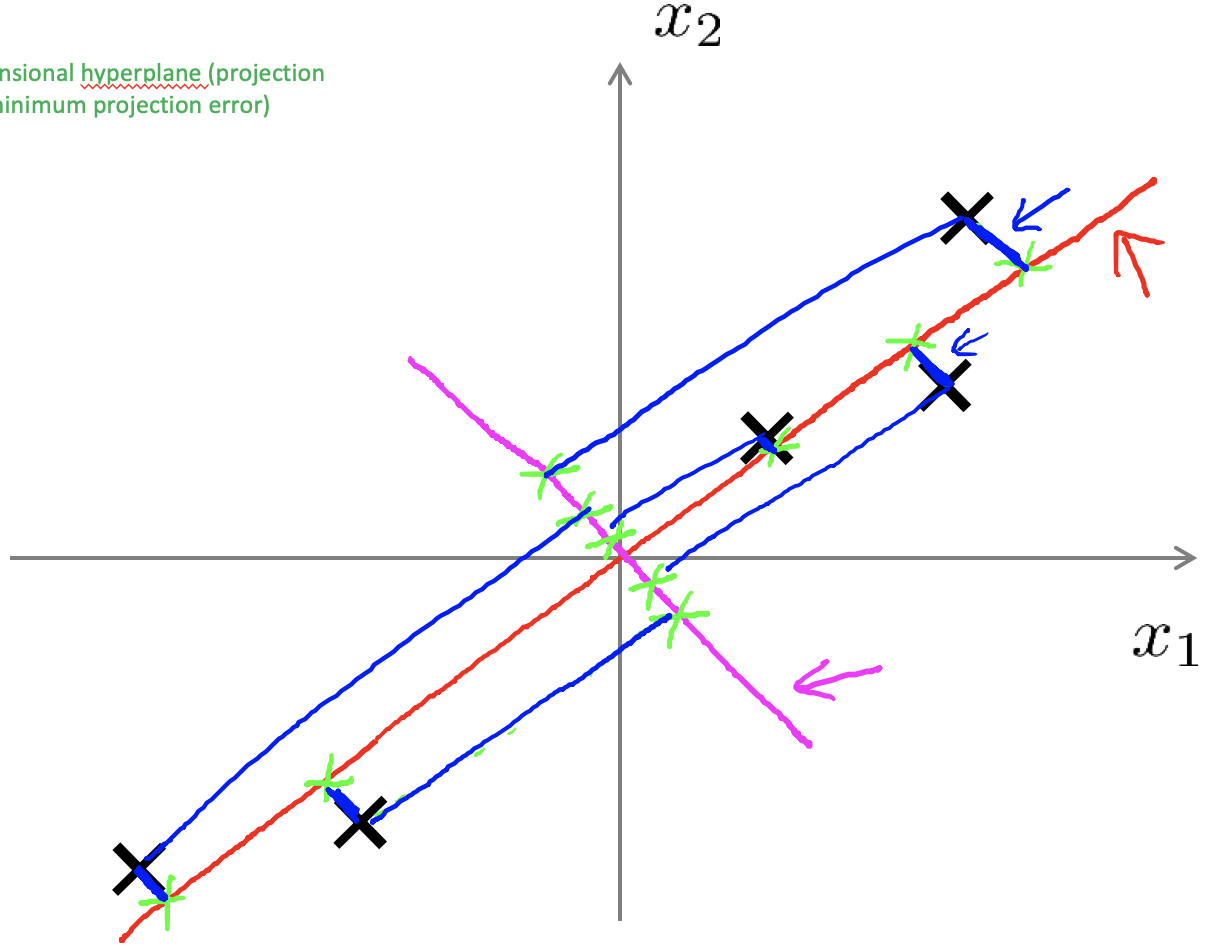
PCA

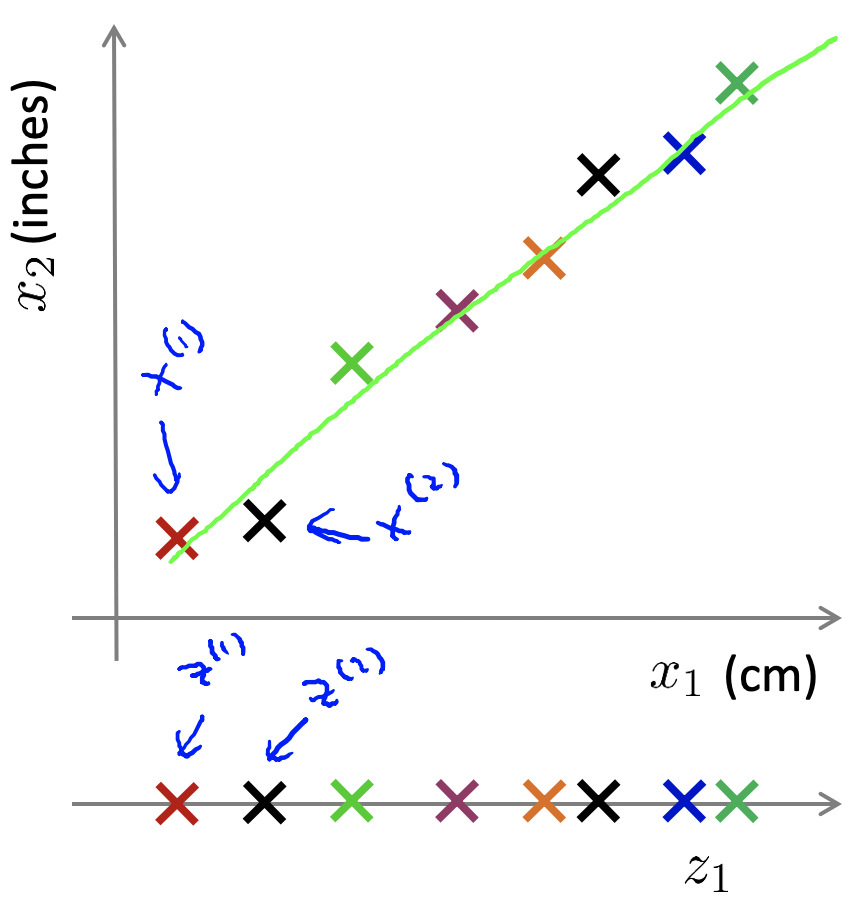
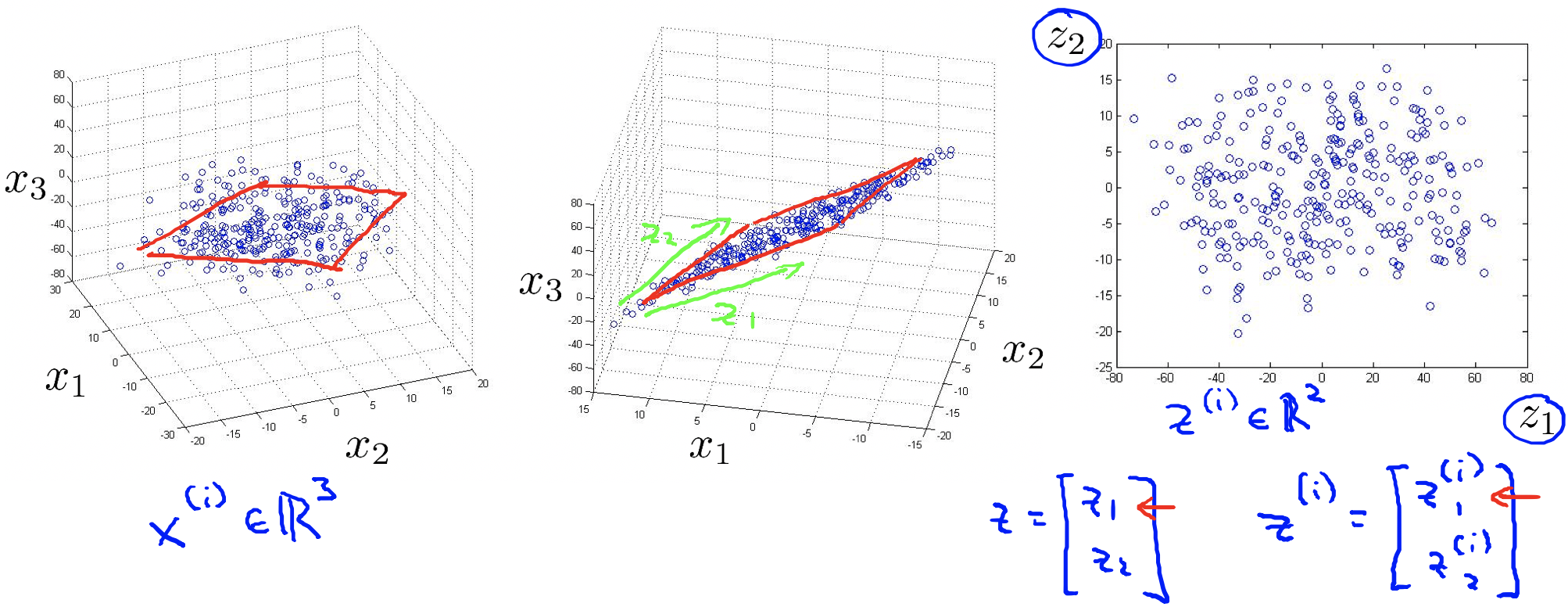
上图是一些数据降维的实例，从2维到1维，从3维到2维。每次降维的过程都会寻找一个基本线或者基本面，大部分数据都从属于这个基本空间上。

PCA算法就是寻找一个投影平面，使得投影误差降到最小。投影误差就是每个数据点到投影线上的距离。图中红线和粉线都可以被视为一个投影线，而红线的投影误差小于粉线的投影误差。 算法过程如下： 1. 将输入数据做尺度缩放和均值归一化，之后用$x_i-\mu_i$来代替数据$x_i$ 2. 计算协方差矩阵$\sum=\frac{1}{m}\times X'\times X$ 3. 计算协方差矩阵的特征向量和特征值 4. 取前k个特征值对应的特征向量，并将其组合成新的矩阵$Z^{(i)}$ 5. 之后将此矩阵与输入数据相乘，得到降维后的数据$U_{reduce}$ 数据恢复的过程为$ x^{(i)}_{approx}=U_{reduce}\cdot Z^{(i)} $ 如何选取k值？ $$ \frac{\frac{1}{m}\sum^m_{i=1}||x^{(i)}-x^{(i)}_{apporx}||^2}{\frac{1}{m}\sum^m_{i=1}||x^{(i)}||^2}\le0.01 $$ 如果上式选取0.01，则说明99%的方差被保留，如果选取0.05，说明95%的方差信息被保留。 使用PCA算法去避免过拟合影响的做法是不可取的，最好是使用正则化。 部署一个机器学习应用时，首先尝试使用原始数据去做，如果达不到效果，再尝试使用PCA方法。 ### 异常检测 在工程实践中，同一类别的数据大部分是分布在一起的，但有少量样本虽然属于同一类别，样本分布却离大部分距离较远，这类样本属于异常样本。 算法在训练的过程中可以通过松弛系数来对异常样本进行处理，但总之异常样本对算法的优化起着副作用的。如何检测出异常样本并忽略它，实际中通常采用正态分布去检测它。 $$ P(x;\mu,\sigma^2)=\frac{1}{\sqrt{2\pi}\sigma}e^-{\frac{(x-\mu)^2}{2\sigma^2}} $$ 当取不同的$\mu$和$\sigma$值时，高斯分布曲线是不一样的。前者影响曲线的中心点，后者影响曲线的面积大小。 **检测算法** 1. 选出你认为可能是异常的特征 2. 拟合参数$\mu$和$\sigma$ 3. 测试新的样本数据，计算$p(x)$ $$ p(x)=\prod^n_{j=1}{p(x_j;\mu_j,\sigma^2_j)} $$ 当$p(x)<\varepsilon$时，即小于某个阈值时，该特征为异常值。 **评估算法**="" 1.="" 计算出适合训练集的参数="" 2.="" 在评估集或者测试集上进行预测，如果$p(x)<\varepsilon$，则为1，否则为0="" 3.="" 计算pr指数或者f1值="" **异常检测算法和监督学习的选择**="" 选择异常检测算法：="" 正样本很少而负样本很多时="" 数据集有很多不同类型的异常样本，而且未来的异常类型可能还与现存的不同="" 从正样本中学习异常样本很难="" 监督学习：="" 拥有大量的正负样本时="" 测试集与训练集相似="" **选择特征**="" 可以对特征进行一些变换，如取$\log$对数，或者取平方根，开方跟等等="" **对异常检测的误差分析**="" 我们希望正常样本的$p(x)$值很大，而异常样本很小。而实际情况两者看不出很大的差别，这时我们可以增加一些特征，将特征维数增高。="" ###="" 推荐系统="" 目标函数：="" $$="" \min\limits_{\theta^{(j)}}\frac{1}{2}\sum_{i:r(i,j)="1}((\theta^{(j)})^Tx^{(i)}-y^{(i,j)})^2+\frac{\lambda}{2}\sum^n_{k=1}(\theta_k^{(j)})^2" 这里需要学习多个参数$\theta^{(i)},\theta^{(2)}…$，所以每次梯度下降时需要对每个参数都进行优化。="" **协同滤波算法**="" 假设一个参数$\theta$，从而估计$x$，之后通过此$x$估计参数$\theta$，以此类推。="" 大规模机器学习="" 数据集比较大的时候，可以采用随机梯度下降或者小批量梯度下降。="" 随机梯度下降：="" 随机打乱顺序="" 每次只关注一个训练样本进行参数更新="" 小批量梯度下降：="" 每次关注少量样本进行参数更新="" 在训练的过程中可以检查梯度是否收敛：="" 取最后1000组样本，求目标函数的平均值，画图="" 若直线抖动幅度较大，增加样本量，再求平均="" 若直线在上升，则减小学习率="" 4.="" 若在最小点周围，可采用变化的学习率=""

在线学习

输入一对样本，更新一次参数，在线更新网络。

应用实例：OCR

Pipeline：

1. 寻找图片上的文字
2. 文字分割
3. 文字分类

总结

监督学习

线性回归、逻辑回归、神经网络、SVM

非监督学习

K-means、PCA、异常检测

特殊应用

推荐系统、大规模机器学习

建立机器学习系统的建议

方差/偏差、正则化、评估算法、学习曲线、错误分析等

赞赏