Support Vector Machine

SVM(Support Vector Machine)，即支持向量机，是一种广泛应用的以监督学习为模式的分类算法。它以边界为出发点，通过最大化边界距离来完成数据分类工作，并使用拉格朗日进行优化，核函数的引入赋予了SVM分类高维特征的力量，最终通过SMO算法有效的实施了SVM的思想。

SVM理论部分

边界概念的引入(Margins)

由逻辑回归可知，$p(y=1|x;\theta)​$的概率由$h_\theta(x)=g(\theta^Tx)​$决定，如果$g(\theta^Tx)\ge0.5​$，即$\theta^Tx\ge0​$，则将被预测为1。所以说$\theta^Tx​$越大，$h_\theta(x)​$就越大，即$\theta^Tx\gg0​$时可以认定$y=1​$，$\theta^Tx\ll0​$时可以认定$y=0​$。

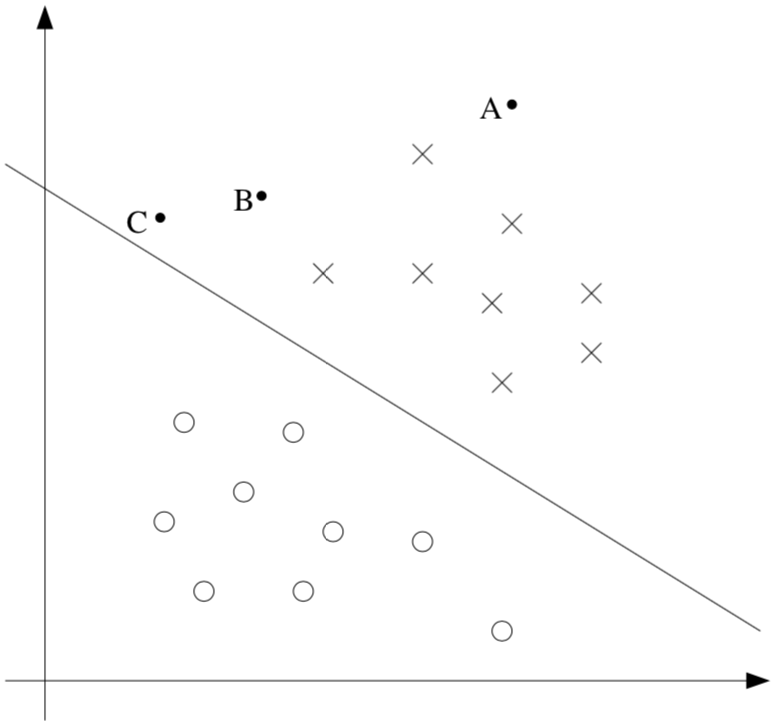
上图中，x表示正样本，o表示负样本，中间的分界线即为决策边界(decision boundary)，也就是$\theta^Tx=0$所划分的线，图中有三个点A、B、C。

A点离决策边界很远，基本上会被分类为正样本，而C点离决策边界很近，很大可能被误分类为负样本。所以说，我们会对A的分类结果很自信，而对于C的分类结果就会产生怀疑。

所以，当给定一组数据进行分类时，我们希望决策边界不光能将数据分类正确，还希望每一个数据都离决策边界非常远，这样就能确信我们的分类结果时正确的。这就是所谓的决策边界。

赋予数据标记

定义类别标签为$y\in\{-1,1\}$，用参数$\omega,b$代替线性分类器中的参数$\theta$，则决策函数为：

$$h_{\omega,b}(x)=g(\omega^Tx+b)=\left\{\begin{aligned}1& \ z\ge0 \\ 0 & \ z<0 \end{aligned}\right. ​$$

符号$b$代替了$\theta_0$，符号$\omega$代替了$[\theta_1…\theta_n]^T$，为了一致性，将$x_0=1$加入到输入特征中。

边界的函数性(Functional)和几何性(Geometric)

函数边界

给定一个训练样本$(x^{(i)},y^{(i)})$，定义函数性边界为：

$$\hat{\gamma}^{(i)}=y^{(i)}(\omega^Tx+b) ​$$

当$y^{(i)}(\omega^Tx+b)>0​$时，说明预测结果是正确的。当函数性边界非常大时，说明此分类模型性能十分好，即：

当$y^{(i)}=1$时，为了让函数性边界非常大，需要$\omega^Tx+b$返回一个非常大的正数值；当$y^{(i)}=-1$时，为了让函数性边界非常大，需要$\omega^Tx+b$返回一个非常小的负数值。

如果仅是将参数$\omega,b$扩大任意尺度，并不会改变$h_{\omega,b}(x)$的值，所以对它们进行任意尺度变化，并不会改变最终的分类性能。

最终的$\hat{\gamma}​$为所有训练集中最小的$\hat{\gamma}^{(i)}​$。

几何边界

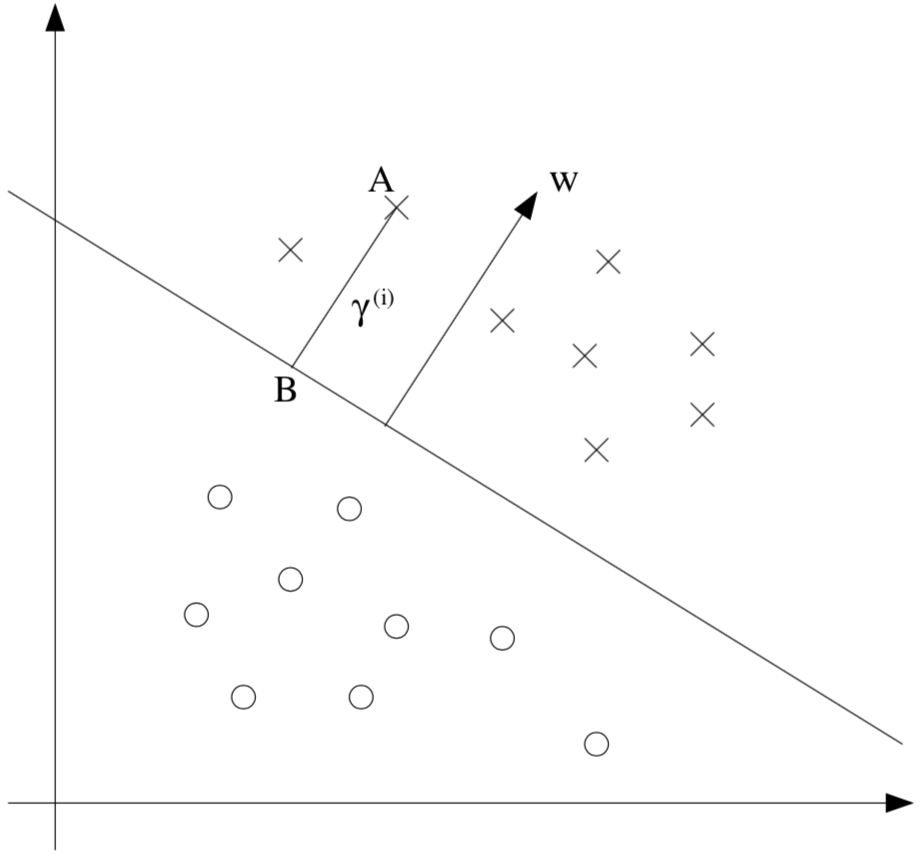
其中，图中A点为正样本，它到决策边界的距离$ \gamma^{(i)}​$是直线段AB的长度。如何去求$ \gamma^{(i)}​$的值呢？

$ \frac{\omega}{\parallel \omega\parallel} $是一个单位长度的向量，与$ \omega $具有相同的方向。假设A点代表$ x^{(i)} $，且B点可以通过$x^{(i)}-\gamma^{(i)}\cdot\frac{\omega}{\parallel \omega\parallel}$来得到。其中B点在决策边界上，所有在决策边界上的数据都满足$w^Tx+b=0$的条件，因此可以得到：

$$w^T(x^{(i)}-\gamma^{(i)}\frac{\omega}{\parallel \omega\parallel})+b=0$$

求解$\gamma^{(i)}$，结果为：

$$w^Tx^{(i)}+b=\gamma^{(i)}\frac{w^Tw}{\parallel \omega\parallel}=\gamma^{(i)}\frac{\parallel \omega\parallel^2}{\parallel \omega\parallel}$$ $$\gamma^{(i)}=\frac{w^Tx^{(i)}+b}{\parallel \omega\parallel}=(\frac{\omega}{\parallel \omega\parallel})^Tx^{(i)}+\frac{b}{\parallel \omega\parallel}$$

给定一个训练样本$(x^{(i)},y^{(i)})​$，定义几何性边界为：

$$\gamma^{(i)}=y^{(i)}((\frac{\omega}{\parallel\omega\parallel})^Tx^{(i)}+\frac{b}{\parallel\omega\parallel}) ​$$

其中当$\parallel\omega\parallel=1​$时，几何性边界和函数性边界一致，通过这种方式将两种边界联合在一起。

边界的优化

如何最大化决策边界，可以通过以下优化方法：

$$max_{\gamma,\omega,b}\ \ \ \gamma ​$$ $$s.t.\ \ \ \ \ \ \ \ \ \ \ \ y^{(i)}(\omega^Tx^{(i)}+b)\ge\gamma,\ \ i=1,…,m​$$ $$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \parallel w\parallel=1 ​$$

然而，由于$\parallel w\parallel=1​$的限制，使得此问题是一个非凸优化，无法使用标准优化方法去求解。为了更好的求解，将上式转变为：

$$max_{\hat{\gamma},\omega,b}\ \ \ \frac{\hat{\gamma}}{\parallel \omega\parallel} ​$$ $$s.t.\ \ \ \ \ \ \ \ \ \ \ \ y^{(i)}(\omega^Tx^{(i)}+b)\ge\hat{\gamma},\ \ i=1,…,m​$$

从此，优化问题转变为最大化$\frac{\hat{\gamma}}{\parallel \omega\parallel} $，并且消除了$\parallel w\parallel=1$的限制。但是目标函数$\frac{\hat{\gamma}}{\parallel \omega\parallel} $仍然是一个非凸优化问题。

由于对参数$\omega,b$可以进行任意尺度的变化，且不影响最终分类器性能。那么我们可以引入一个比例约束，通过限制参数$\omega,b$使得训练集的函数边界为1，即$\hat{\gamma}=1$。

那么最大化$\frac{\hat{\gamma}}{\parallel \omega\parallel}$就可以转化为最大化$\frac{1}{\parallel \omega\parallel}$，也就等于最小化$\parallel \omega\parallel^2$，即：

$$min_{\omega,b}\ \ \ \ \ \ \frac{1}{2}\parallel \omega\parallel^2 ​$$ $$s.t.\ \ \ \ \ \ \ \ \ \ \ \ y^{(i)}(\omega^Tx^{(i)}+b)\ge1,\ \ i=1,…,m​$$

这样就把无法优化的问题有效的解决了，上式是一个线性约束的二次凸优化问题，给予了我们解决优化边界分类器的方法。接下来使用拉格朗日方法去解决这个问题。

拉格朗日算子

拉格朗日乘法是为了解决如下问题：

$$min_\omega\ \ \ f(\omega)$$ $$s.t.\ \ \ \ \ h_i(\omega)=0,\ \ i=1,…,l.$$

1. 定义拉格朗日式为：

$$\mathcal{L}(\omega,\beta)=f(\omega)+\sum^l_{i=1}\beta_ih_i(\omega) ​$$

其中，$\beta_i$称为拉格朗日乘数。

1. 将$\mathcal{L}$的偏导设为零，求解参数$\omega,\beta$：

$$\frac{\partial{\mathcal{L}}}{\partial{\omega_i}}=0,\frac{\partial{\mathcal{L}}}{\partial{\beta_i}}=0$$

对偶问题

假设要优化以下问题，称之为 primal 问题：

$$min_{\omega}\ \ \ \ \ \ \ \ \ f(\omega)$$ $$s.t.\ \ \ \ \ \ \ \ \ \ \ \ g_i(\omega)\le0,\ \ i=1,…,k$$ $$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ h_i(\omega)=0,\ \ i=1,…,l.$$

首先定义拉格朗日式为：

$$\mathcal{L}(\omega,\alpha,\beta)=f(\omega)+\sum^k_{i=1}\alpha_ig_i(\omega)+\sum^l_{i=1}\beta_ih_i(\omega) ​$$

其中，$\alpha_i,\beta_i$为拉格朗日乘数。

定义$\theta_{primal}(\omega)=\underset{\alpha,\beta:\alpha_i\ge0}{max}\mathcal{L}(\omega,\alpha,\beta)​$，给定某些$\omega​$，如果违反了约束限制，则：

$$\theta_{primal}(\omega)=\underset{\alpha,\beta:\alpha_i\ge0}{max}f(\omega)+\sum^k_{i=1}\alpha_ig_i(\omega)+\sum^l_{i=1}\beta_ih_i(\omega)=\infty ​$$

如果满足了约束条件，则$\theta_{primal}=f(\omega)$。所以，$\theta_{primal}$ 在$\omega$满足约束的时候与所要优化的问题拥有相同的结果，所以按照 primal 问题所示，得到以下最小化问题：

$$\underset{\omega}{min}\ \theta_{primal}=\underset{\omega}{min}\ \underset{\alpha,\beta:\alpha_i\ge0}{max} \mathcal{L}(\omega,\alpha,\beta) ​$$

它与 primal 优化问题一致。

定义$\theta_{dual}(\alpha,\beta)=\underset{\omega}{min}\ \mathcal{L}(\omega,\alpha,\beta)$，上述 primal 问题是关于参数$\alpha,\beta$的最大化问题，而此问题是关于参数$\omega$的最小化问题，如果加上 primal 问题的限制，变为 dual 优化问题：

$$\underset{\alpha,\beta:\alpha_i\ge0}{max}\ \theta_{dual}(\alpha,\beta)=\underset{\alpha,\beta:\alpha_i\ge0}{max}\ \underset{\omega}{min}\ \mathcal{L}(\omega,\alpha,\beta) ​$$

这就转化为与 primal 问题加上最小化问题一致了，只是把最大化和最小化的位置进行了颠倒，然后 primal 和 dual 问题可以产生以下相关性：

$$\underset{\alpha,\beta:\alpha_i\ge0}{max}\ \underset{\omega}{min}\ \mathcal{L}(\omega,\alpha,\beta) \ \le\ \underset{\omega}{min}\ \underset{\alpha,\beta:\alpha_i\ge0}{max} \mathcal{L}(\omega,\alpha,\beta)$$

特殊情况下，上式取等号。

基于以上假设，肯定存在参数$ \omega^* $是 primal 问题的结果，$ \alpha^* , \beta^* $是 dual 问题的结果，或者存在同时是 primal 和 dual 两个问题的结果，只要它满足 KKT 条件，即：

$$\frac{\partial}{\partial{\omega_i}}\mathcal{L}(\omega^*,\alpha^*,\beta^*)=0,\ \ i=1,…,n ​$$ $$\frac{\partial}{\partial{\beta_i}}\mathcal{L}(\omega^*,\alpha^*,\beta^*)=0,\ \ i=1,…,l ​$$ $$\ \ \ \ \ \ \ \ \ \ \ \ \ \alpha^*_ig_i(\omega^*)=0,\ \ i=1,…,k$$ $$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ g_i(\omega^*)\le0,\ \ i=1,…,k$$ $$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \alpha^*\ge0,\ \ i=1,…,k$$

这里隐含着一个条件，当$\alpha>0$时，$g(\omega^*)=0$。这是一个关键条件，表明支持向量机仅有少量的 support vectors。

分类器的优化

首先可以把边界的优化函数中约束条件改为：

$$g_i(\omega)=1-y^{(i)}(\omega^Tx^{(i)}+b)\le0$$

则拉格朗日式为：

$$\mathcal{L}(\omega,b,\alpha)=\frac{1}{2}\parallel \omega\parallel^2-\sum^m_{i=1}\alpha_i[y^{(i)}(\omega^Tx^{(i)}+b)-1] ​$$

为了优化此函数，需要先进行关于参数$\omega,b​$的最小化$\mathcal{L}​$工作，去得到$\theta_{dual}​$，即求关于两个参数的偏导并置为零：

$$\bigtriangledown_\omega\mathcal{L}(\omega,b,\alpha)=\omega-\sum^m_{i=1}\alpha_iy^{(i)}x^{(i)}=0​$$

即$\omega=\sum^m_{i=1}\alpha_iy^{(i)}x^{(i)}​$

$$\bigtriangledown_b\mathcal{L}(\omega,b,\alpha)=\sum^m_{i=1}\alpha_iy^{(i)}=0$$

即$\sum^m_{i=1}\alpha_iy^{(i)}=0$

将以上结果代入原式：

$$\mathcal{L}(\omega,b,\alpha)=\sum^m_{i=1}\alpha_i-\frac{1}{2}\sum^m_{i,j=1}y^{(i)}y^{(j)}\alpha_i\alpha_j(x^{(i)})^Tx^{(j)} ​$$

这样我们得到关于参数$\omega,b$的最小化的优化结果，将其与另两个约束条件结合，得到 dual 优化问题：

$$\underset{\alpha}{max}\ Dual(\alpha)=\sum^m_{i=1}\alpha_i-\frac{1}{2}\sum^m_{i,j=1}y^{(i)}y^{(j)}\langle x^{(i)},x^{(j)}\rangle ​$$ $$s.t.\ \ \alpha_i\ge0,\ \ i=1,…,m$$ $$\ \ \ \ \ \ \ \ \sum^m_{i=1}\alpha_iy^{(i)}=0 ​$$

最后，在分类预测的时候，给定输入数据$x$，通过上面求得的关于参数$\omega$的等式，可得：

$$\omega^Tx+b=(\sum^m_{i=1}\alpha_iy^{(i)}x^{(i)})^Tx+b=\sum^m_{i=1}\alpha_iy^{(i)}\langle x^{(i)},x\rangle+b$$

其中，$\langle x^{(i)},x\rangle$是将训练集中每个点与输入数据$x$做内积，而有先前可知，仅仅当训练集中的数据是支持向量时，$\alpha_i$才大于零，其它皆为零，所以可以忽略这些，仅考虑将输入数据与支持向量做内积即可，并且支持向量的个数是非常少的。

核函数

将输入空间映射到另一个空间域的方法就是使用核函数，这种映射关系用$\phi(x)$表示。给定一个特征映射函数$\phi$，定义相关核为：

$$K(x,z)=\phi(x)^T\phi(z)$$

即在算法中当遇到$\langle x,z\rangle$时可以用$K(x,z)$来代替。

但是$K(x,z)​$的计算量很大，而且$\phi(x)​$的计算量也很大。解决方法是我们可以让 SVM 直接在$\phi​$的高维空间去学习，不需要去计算$\phi(x)​$。

如果$\phi(x)$和$\phi(z)$很相似，那么其$K(x,z)$值就会很大，否则则很小，那么就可以通过高斯很函数来判断它俩的相似性：

$$K(x,z)=exp(-\frac{\parallel x-z\parallel^2}{2\sigma^2})$$

当核矩阵是对称半正定时，可以说明$K$是一个有效的核。

正则化和不可分实例

当得到一个决策边界时，如果加入一个数据会导致决策边界发生很大的变化，那么可能会导致不好的分类结果。为了解决此问题，不对那些异常值敏感，那么可以使用正则化方法：

$$min_{\gamma,\omega,b}\ \ \ \ \ \ \frac{1}{2}\parallel \omega\parallel^2+C\sum^m_{i=1}\xi_i,\ \ i=1,…,m$$ $$s.t.\ \ \ \ \ \ \ \ \ \ \ \ y^{(i)}(\omega^Tx^{(i)}+b)\ge1-\xi_i,\ \ i=1,…,m$$ $$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \xi_i\ge0,\ \ i=1,…,m.$$

此时，某些异常点被允许边界小于1，如果一个实例的函数边界为$1-\xi_i$，可以对目标函数通过增加$C\xi_i$来进行一个惩罚，参数$C$控制了相关权重与最小化$\parallel \omega\parallel^2$的关系，确保大部分实例数据的函数边界至少为1。

以上，可以把拉格朗日式改为：

$$\mathcal{L}(\omega,b,\xi,\alpha,r)=\frac{1}{2}\parallel \omega\parallel^2+C\sum^m_{i=1}\xi_i-\sum^m_{i=1}\alpha_i[y^{(i)}(\omega^Tx^{(i)}+b)-1+\xi_i]-\sum^m_{i=1}r_i\xi_i$$

其中，参数$\alpha_i,r_i$是拉格朗日乘子，约束其必须大于等于零。

求偏导之后，所得的 dual 优化问题为：

$$\underset{\alpha}{max}\ Dual(\alpha)=\sum^m_{i=1}\alpha_i-\frac{1}{2}\sum^m_{i,j=1}y^{(i)}y^{(j)}\langle x^{(i)},x^{(j)}\rangle$$ $$s.t.\ \ 0\le\alpha_i\le C,\ \ i=1,…,m$$ $$\ \ \ \ \ \ \ \ \sum^m_{i=1}\alpha_iy^{(i)}=0 ​$$

则 KKT 条件可转化为：

$$\ \ \ \ \ \ \ \ \alpha_i=0\ \Rightarrow\ y^{(i)}(\omega^Tx^{(i)}+b)\ge1 ​$$ $$\ \ \ \ \ \ \ \ \alpha_i=C\ \Rightarrow\ y^{(i)}(\omega^Tx^{(i)}+b)\le1 ​$$ $$0<\alpha_i<C\ \Rightarrow\ y^{(i)}(\omega^Tx^{(i)}+b)=1$$

SMO算法

SMO(sequential minimal optimization)算法提供了一种有效的方式去解决 dual 问题。

当使用函数去优化参数时，可以固定其中一个参数，优化另一个参数，直到达到目标点来完成任务。假设参数$\alpha_i$满足约束条件，如果固定$\alpha_2,…,\alpha_m$仅调整$\alpha_1$，是否能达到优化目的？

答案是否定的，因为参数$\alpha_1y^{(1)}=-\sum^m_{i=2}\alpha_iy^{(i)}$，但改变一次，可能其它所有参数都会发生改变，就不满足我们的方法条件。

因此，如果要更新参数$\alpha_i$，必须要至少同时更新两个参数才能保证不违反约束条件，所以 SMO 算法可以简单的分为以下步骤：

Repeat till convergence {

​ 1 选择一堆参数$\alpha_i,\alpha_j$去更新

​ 2 重新计算优化函数 dual ，固定剩下的参数

}

为了测试算法的趋势，可以在优化的过程中检查其是否满足 KKT 情况。SMO 算法有效的另一个原因是更新那两个参数的计算十分快。

固定两个参数后，可得：

$$\alpha_1y^{(i)}+\alpha_2y^{(2)}=-\sum^m_{i=3}\alpha_iy^{(i)} ​$$

右边参数是固定的，只能调整左边，意味着：

$$\alpha_1y^{(i)}+\alpha_2y^{(2)}=\zeta$$ $$\alpha_1=(\zeta-\alpha_2y^{(2)})y^{(1)}$$ $$Dual(\alpha_1,\alpha_2,…,\alpha_m)=Dual((\zeta-\alpha_2y^{(2)})y^{(1)},\alpha_2,…,\alpha_m)$$

赞赏