本文主要总结排序算法。

排序算法 平均时间复杂度 最坏复杂度 空间复杂度 稳定性
冒泡排序 $ O(N^2) $ $ O(N^2) $ $ O(1) $ 稳定
选择排序 $ O(N^2) $ $ O(N^2) $ $ O(1) $ 不稳定
插入排序 $ O(N^2) $ $ O(N^2) $ $ O(1) $ 稳定
快速排序 $ O(N\log(N)) $ $ O(N^2) $ $ O(1) $ 不稳定
归并排序 $ O(N\log(N)) $ $ O(N\log(N)) $ $ O(1) $ 稳定
堆排序 $ O(N\log(N)) $ $ O(N\log(N)) $ $ O(1) $ 不稳定
希尔排序 $ O(N\log(N)) $ $ O(N\log(N)) $ $ O(1) $ 不稳定

冒泡排序

基于比较的排序算法，优点是稳定、实现简单、N较少时性能良好。

原理

遍历整个数组，相邻的两个数据进行比较，小的放在前面，大的放在后面，如此类推，直到排序完成。

  • $ O(1) $的额外空间
  • $ O(N^2) $次比较
  • $ O(N^2) $次交换
  • 自适应性

代码

1
2
3
4
5
6
7
8
9
10
11
void bubble_sort(int a[], int len)
{
       	for (int i = 0; i < len-1; i++)
       	{
		for (int j = len-1; j > i; j--)
		{
				if (a[j] < a[j-1])
				swap(a, j-1, j);
		}
       	}
}

分析

冒泡排序在几乎排序的情况下只需$ O(N) $的时间复杂度，与插入排序具有很多相同的属性，但开销略高，表现在至少需要遍历数组2次，而插入接近1次。

冒泡排序中若数据排序好了，仍会继续进行下一轮的比较，这是没有意义的，可以在每次迭代的过程中（代码中第4、5行间）插入一个标志变量flag，若在此轮迭代中发生交换操作，则置flag为1，若此轮迭代的flag为0则停止迭代。

演示图

  • 随机情况下
  • 接近排序的情况下
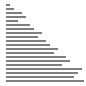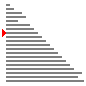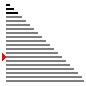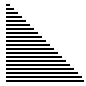
  • 最差情况下

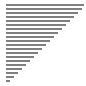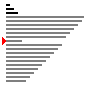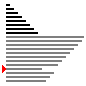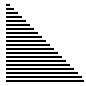
选择排序

最简单直观的排序，与冒泡排序有些类似，都是在每次迭代中把最小的数放在前面，但过程不同，它是通过对整体数组的选择。选择排序是不稳定的排序。

原理

每次迭代中，遍历数组，找出最小的数，放在最前面，之后迭代除第一个数以外的所有元素，迭代到最后两个数，排序完成。

  • $ O(1) $的额外空间
  • $ O(N^2) $次比较
  • $ O(N) $次交换
  • 没有自适应性

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void select_sort(int a[], int len)
{
	for (int i = 0; i < len-1; i++)
	{
		int minIndex = i;
		for (int j = i+1; j < len; j++)
		{
			if (a[j] < a[minIndex])
				minIndex = j;
		}
		if (minIndex != i)
			swap(a, i, minIndex);
	}
}

分析

选择排序相比于冒泡排序最大的区别在于它每次只有在确定了当前数组中最小数的情况下才会进行交换操作，大大减少了交换次数。

演示图

  • 随机情况下
  • 接近排序的情况下
  • 最差情况下

插入排序

插入排序不需要通过比较来达到排序目的的，它是通过找当前元素在排序数组中合适的位置，将它插入到那个合适的位置来完成任务的。插入排序是稳定的排序。

原理

将数据分为有序部分和无序部分，初始化时有序部分为第一个元素，之后依次将无序部分的每个元素插入到有序部分中合适的位置，直到所有元素都在有序部分中。

  • $ O(1) $的额外空间
  • $ O(N^2) $次比较
  • $ O(N^2) $次交换
  • 自适应性

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void insert_sort(int a[], int len)
{
    for (int i = 1; i < len; i ++)
    {
        int j = i - 1;
        int k = a[i];
        while (j > -1 && k < a[j] )
        {
            a[j+1] = a[j];
            j--;
        }
        a[j+1] = k;
    }
}

分析

插入排序在几乎排序的情况下只需$ O(N) $的时间复杂度，开销很低。每次进行插入的时候都保证前面的数已经有序。

演示图

  • 随机情况下
  • 接近排序的情况下
  • 最差情况下

快速排序

快速排序是表现最好的排序算法，思想来自冒泡排序。快速排序是通过比较并交换小数和大数，之后小数就会浮在上面，而大数会落在下面。快速排序在初始时要设定一个基准数，同时快速排序也是不稳定的。

原理

首先从序列中设定一个基准数，将小于它的数放在它的左边，大于它的数放在右边。之后对左右两边的序列重复进行上述操作，直到各区间只有一个元素。

  • $ O(\log(N)) $的额外空间
  • $ O(N^2) $的时间复杂度
  • 一般是$ O(N*\log(N)) $的时间复杂度
  • 没有自适应性

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
void quick_sort(int a[], int left, int right)
{
	if (left < right)
	{
		int i = left, j = right, target = a[left];
		while (i < j)
		{
			while (i < j && a[j] > target)
				j--;
			if (i < j)
				a[i++] = a[j];
			while (i < j && a[i] < target)
				i++;
			if (i < j)
				a[j] = a[i];
		}
		a[i] = target;
		quick_sort(a, left, i-1);
		quick_sort(a, i+1, right);
	}
}

分析

快速排序的主要思想：冒泡+二分+递归分治。

演示图

  • 随机情况下
  • 接近排序的情况下
  • 最差情况下

归并排序

归并排序是稳定的排序算法，它是分治法的一个典型应用。首先归并排序将序列进行递归二分，之后将每个排好序的区间进行归并操作完成排序任务。

原理

将序列进行二分操作，直到每个区间只有一个元素时停止，这时可以认为每个区间都是有序的。之后进行归并操作，合并相邻两个区间，直到所有元素排好序为止。

  • $ \Theta(N) $的额外空间
  • $ \Theta(\log(N)) $的额外空间（使用链表）
  • $ \Theta(N*\log(N)) $的时间复杂度
  • $ O(N) $的空间复杂度
  • 没有自适应性
  • 不需要随机访问数据

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
void merge(int arr[], int temp_arr[], int start_index, int mid_index, int end_index)
{
    int i = start_index, j = mid_index + 1;
    int k = 0;
    while (i < mid_index+1 && j < end_index+1)
    {
        if (arr[i] > arr[j])
            temp_arr[k++] = arr[j++];
        else
            temp_arr[k++] = arr[i++];
    }
    while (i < mid_index+1)
    {
        temp_arr[k++] = arr[i++];
    }
    while (j < end_index+1)
        temp_arr[k++] = arr[j++];

    for (i = 0, j = start_index; j < end_index+1; i++, j++)
        arr[j] = temp_arr[i];
}

void merge_sort(int a[], int temp_a[], int start_index, int end_index)
{
    if (start_index < end_index)
    {
        int mid_index = (start_index + end_index) / 2;
        merge_sort(a, temp_a, start_index, mid_index);
        merge_sort(a, temp_a, mid_index+1, end_index);
        merge(a, temp_a, start_index, mid_index, end_index);
    }
}

分析

归并排序的主要思想就是先递归分解序列，再合并序列。合并的过程时主要过程，要逐次比较每个位置，建立一个临时数组，谁小就先放入临时数组中，同时指针往后移一个。

演示图

  • 随机情况下
  • 接近排序的情况下
  • 最差情况下

堆排序

堆排序在Top k问题中使用频繁，采用二叉堆的数据结构来实现，二叉堆是一个近似的完全二叉树。堆排序是不稳定的排序算法。

二叉堆具有一些性质：

  1. 父节点的key大于等于任何一个子节点的key
  2. 每个节点的左右子树都是一个二叉堆

原理

对二叉堆数组通过移除根节点进行有序化。首先将heap[0]与heap[N-1]交换，对heap[0…N-2]做最大堆调整。之后将heap[0]与heap[N-2]交换，对heap[0…N-3]做最大堆调整，以此类推，直到heap[0]与heap[1]交换。由于每次都是将最大数并入到后面的有序区间内，所以整个数组变得有序。

  • $ O(1) $的额外空间
  • $ O(N*\log(N)) $的时间复杂度
  • 没有自适应性

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
void heap_maxAdjust(int a[], int i, int len)
{
	int child;
	int temp;	
	for (; 2*i+1 < len; i = child)
	{
        	child = 2 * i + 1;
        	if (child < len-1 && a[child+1] > a[child])
			child++;

        	if (a[i] < a[child])
			swap(a, i, child);
        	else
            		break;
	}
}

void heap_sort(int a[], int len)
{
	int i;
	for (int i = len/2-1; i >= 0; i--)
		heap_maxAdjust(a, i, len);

	for (i = len-1; i > 0; i--)
	{
		swap(a, 0, i);
		heap_maxAdjust(arr, 0, i);
	}
}

分析

当对二叉堆进行了最大堆调整后，就可以直接找出最大的几个数，也就解决了Top k的问题。

演示图

  • 随机情况下
  • 接近排序的情况下
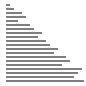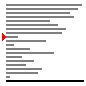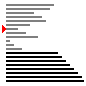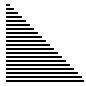
  • 最差情况下

希尔排序

希尔排序，也称递减增量排序，思想是分组插入排序，它是不稳定的排序算法。
希尔排序是插入排序的一种高效率的实现。

原理

将数组列在一个矩阵表中，对矩阵表中每一列的元素进行插入排序，行数代表步长，步长随着递归而减小，直到只有一列。

  • $ O(1) $的额外空间
  • $ O(N^\frac{3}{2}) $的时间复杂度
  • 自适应性

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
void shell_insert(int a[], int len, int d) 
{
	for(int i = d; i < len; i++) 
	{
		int j = i - d;
		int temp = a[i]; 
		while (j >= 0 && arr[j] > temp) 
		{
		    a[j+d] = a[j]; 
		    j -= d;
        	}
        	if (j != i - d)
            		a[j+d] = temp;
    	}
}

void shell_sort(int a[], int len) 
{
	int d = len / 2;
	while(d > 0) 
	{
		shell_insert(a, d, len);
        	d /= 2;
    	}
}

分析

代码中的 d 为步长，从数组长度的一半开始，每次减半，直到为0。步长的选择直接决定了希尔排序的复杂度。希尔排序在接近排序的情况下只需$ O(N*\log(N)) $的时间复杂度。

演示图

  • 随机情况下
  • 接近排序的情况下
  • 最差情况下

参考文献

https://www.toptal.com/developers/sorting-algorithms

https://www.jianshu.com/p/f5baf7f27a7e

http://wuchong.me/blog/2014/02/09/algorithm-sort-summary/