Decision Tree

决策树是运用于分类任务的一种树形结构，其中每个内部节点代表某一属性特征，叶节点代表某个类别。决策树的决策过程从根节点开始，将数据与特征节点进行比较，并根据结果选择下一分支，直到叶节点作为最终的分类结果。

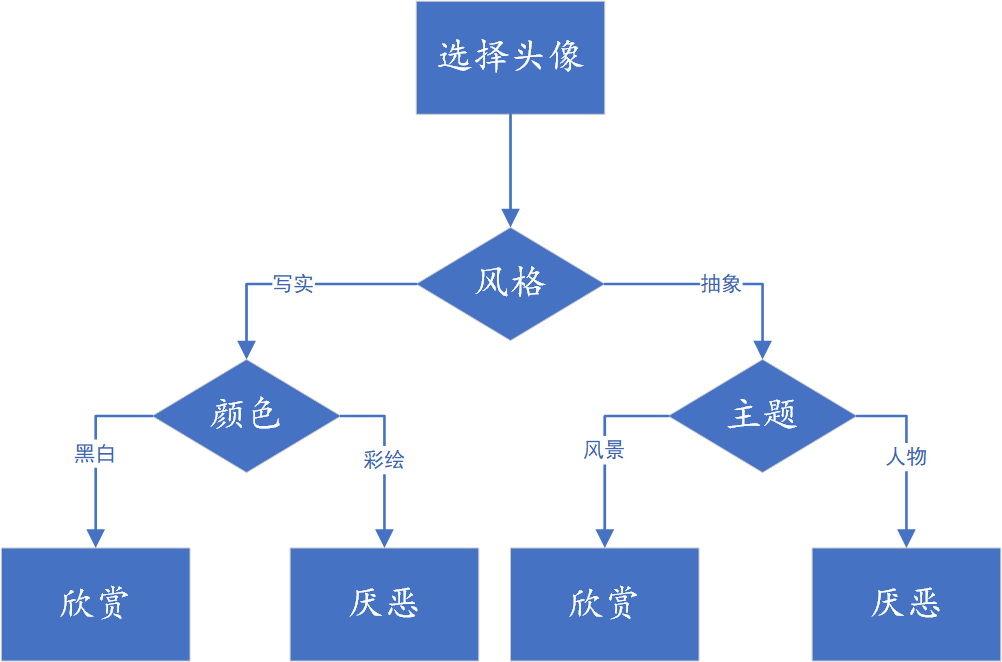
决策树算法过程

1. 特征节点选择：从训练数据的特征中选择一个特征作为当前节点的分裂依据；
2. 决策树生成：根据所有特征评估标准，从上至下递归生成子节点，直到数据不可分为止；
3. 剪枝：应对过拟合问题，通过剪枝来缩小树的结构和规模。

ID3算法

算法介绍

ID3算法的目的是决策树在分裂的时候，能够使得分裂之后的两个分支最终所能代表不同的类别，即分类之后节点的”纯度”越来越高。为了衡量分裂之后节点的”纯度”，使用信息熵这个指标，选取使得信息熵增益最大的节点特征进行分裂。

样本集合$D$中第$k$类样本所占比例为$p_k​$，则信息熵的定义如下：

$$I(D)=-\sum^{|y|}_{k=1}p_k\log_2^{p_k}$$

节点属性$x$有$N$个可能的取值，即${x_1,x_2,x_3,…,x_n}$，而在样本集合$D$中，属性$x$中取值为$x_n$的样本集合记为$D_n$，则利用节点属性$x$对样本集合$D$进行划分所能得到的信息增益为：

$$G(D,a)=I(D)-\sum_{n=1}^{N}\frac{|D_n|}{|D|}I(D_n)$$

信息增益即表示当知道节点属性$x$的信息时，使得样本集合不确定性减少的程度。所以在ID3算法中，决策树中每个节点是否进行分裂取决于分裂之后的信息增益是否最大化。

算法缺陷

当某种类别可取值数目较多时，信息增益属性能够有效衡量分裂的好坏。但是当某种类别只取一种值时，条件熵为零，则信息增益就无法取得好的效果。

C4.5算法

算法介绍

C4.5算法利用信息增益率这个指标来衡量节点分裂的好坏，它是将信息增益和属性的固有值综合考虑而产生的指标。

属性$x$的固有值能够反映出此节点属性最终能够分成的类别数目，当选取$x$作为分裂节点，最终通过此节点所得到的类别数目越多，此节点的固有值就越大，公式如下：

$$IV(x)=-\sum^N_{n=1}\frac{|D_n|}{|D|}\log_2^{\frac{|D_n|}{|D|}}$$

为了改善ID3算法，使得当此节点进行分裂所得到的类别数目越多时，即表明此节点的分裂”纯度”越低，则信息增益率可写为：

$$G_{ratio}(D,x)=\frac{G(D,x)}{IV(x)}$$

而信息增益率其实是对可取类别数目较少的节点特征有所偏爱，即这个节点所得到的类别数目越少，就在此节点进行分裂，容易导致边缘化和极端化。所以C4.5算法不直接采用信息增益率这个判别指标，而是首先选取节点属性的信息增益率高于平均水平的那些作为候选节点，之后从这些候选节点中选择信息增益最高的那个节点作为当前分裂节点。

赞赏